Formulaire de mathématiques
Vous trouverez sur cette page un ensemble de fiches pratiques vous permettant de réviser facilement les domaines de mathématiques vus au lycée en première et terminale. Chaque paragraphe de cette page contient l'essentiel des connaissances à retenir ainsi que toutes les formules à connaître.
IMPORTANT : il va de soit que dans toutes les expressions algébriques exposées sur cette page les fractions n'ont de sens et ne sont valables que dans le cas où leur dénominateur est non nul, même si cette condition n'est pas systématiquement rappelée.
Les identités remarquables
Le carré d'une somme :
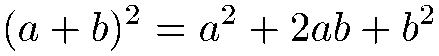
![]()
Le cube d'une somme :
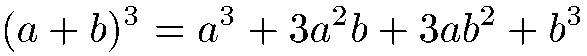
Une somme à la puissance 4 :
![]()
Une somme à la puissance 5 :
![]()
La différence de deux carrés :
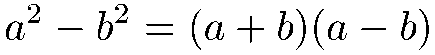
Les puissances
Dans toutes les expressions
ci-dessous, les nombres x, a, b, n et m peuvent ête n'importe quels nombres
réels.
Les exposants ne sont donc pas forcément des nombres entiers.
Voici les 3 propriétés de base des puissances :
L'exposant est une somme :
![]()
L'exposant est une différence (avec x non nul) :
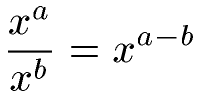
L'exposant est un produit :
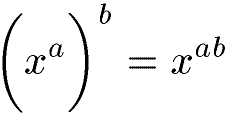
Cas des puissances négatives ou inverses :
L'exposant est l'opposé d'un nombre (avec x non nul) :
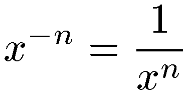
L'exposant est l'inverse d'un nombre (racine nième, avec n non nul) :
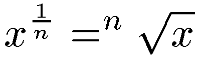
L'exposant est une fraction :
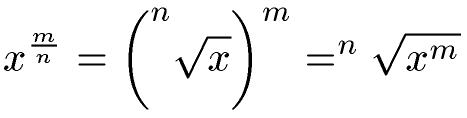
Et voici 3 cas particuliers à connaître :
Cas où l'exposant vaut 0 :
![]()
Tout nombre élevé à la puissance zéro est égal à 1
Cas où l'exposant vaut 0,5 :
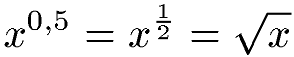
Calculer la racine carrée d'un nombre revient à élever ce nombre à la puissance 0,5
Cas où l'exposant vaut 1 :
![]()
Tout nombre élevé à la puissance 1 est égal au nombre lui-même
L'équation du second degré ax²+bx+c = 0
Dans l'équation algébrique du second degrés suivante, a, b et c sont 3 nombres réels :
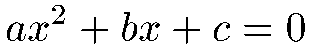
Résoudre cette équation revient à trouver les valeurs de x pour lesquelles l'équation est vraie.
Méthode de résolution de l'équation du second degrés :
1) On calcule le discriminant Delta :
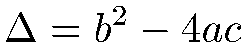
2) Si Delta
est positif, il existe 2 racines réelles, x1 et x
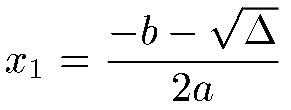
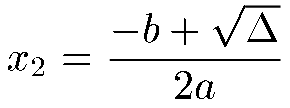
Il existe 2 relations
entre les racines x1 et x
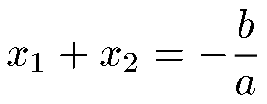
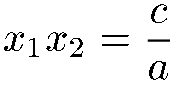
Si on appelle P(x) le polynome du second degrés, il existe 2 manière de factoriser P(x) lorsque Delta est positif :
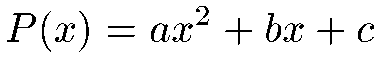
Première factorisation : la factorisation par a :
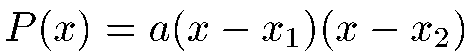
Deuxième factorisation : la factorisation par c :
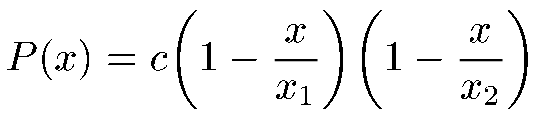
3) Si Delta
est égal à zéro, il existe une seule racine x0,
appelée 'racine double'
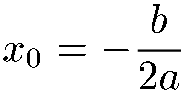
Dans le cas où Delta est nul, la factorisation du polynome P(x) est la suivante :
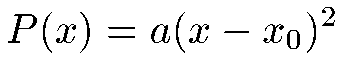
4) Si Delta est négatif, il n'existe aucune racine réelle pour l'équation, et le polynome n'est pas factorisable.
Incroyable mais vrai !
Pour enfin tout comprendre sur l'intégration par changement de variable !
Retrouver toutes les techniques de recherche rapide des racines d'un polynome de degré quelconque
Comment calculer cos(pi/n) en utilisant le triangle de Pascal ?
Relations trigonotmétriques
La formule d'Euler :
Un nombre complexe de module 1 et d'argument x peut s'écrire de la manière suivante
![]()
Conséquence de la formule d'Euler :
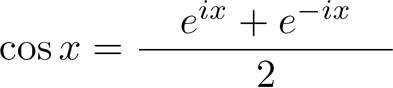
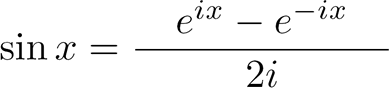
La formule de Moivre :
Un nombre complexe de module 1 et d'argument x, élevé à la puisssance n, peut s'écrire de la manière suivante
![]()
Technique de linéarisation
Une expression est dite linéarisée si elle ne comporte aucun produit de fonctions circulaires.
La linéarisation
consiste à exprimer |
en fonction
de |
ou de |
Voyons un
exemple concret en linéarisant |
Nous allons ainsi démontrer la relation suivante :
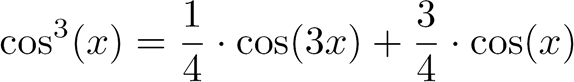
On commence en utilisant la formule d'Euler :
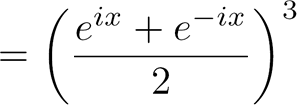 |
||
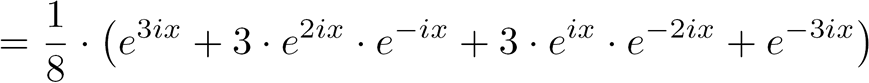 |
||
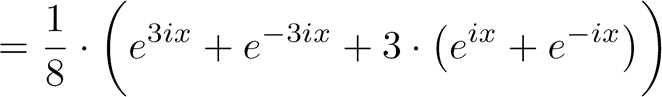 |
||
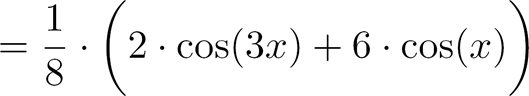 |
| On en déduit l'expression linéarisée de | suivante : |
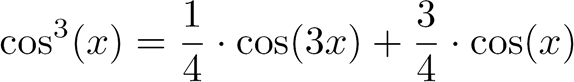
Rappel complémentaire, utile pour la linéarisation :
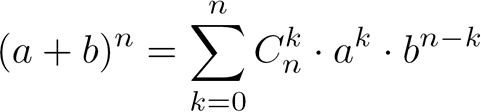
avec
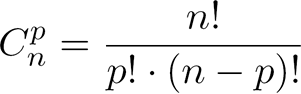
Technique de décomposition
La décomposition
consiste à exprimer |
en fonction
de |
ou de |
Voyons un
exemple concret en décomposant |
Nous allons ainsi démontrer la relation suivante :
![]()
On commence en utilisant la formule d'Euler :
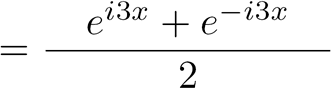 |
||
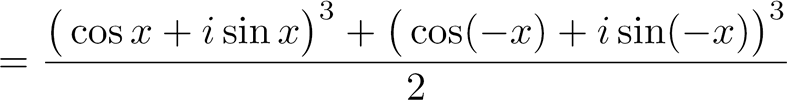 |
||
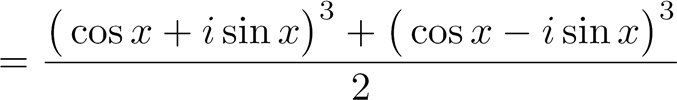 |
||
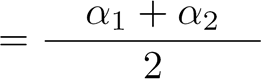 |
Avec :
![]()
![]()
On remarque que les nombres Alpha 1 et Alpha 2 sont des complexes conjugués :
![]()
Calcul de Alpha 1 et de Alpha 2 :
![]()
![]()
La somme Alpha 1 + Alpha 2 est un nombre réel :
![]()
Il faut maintenant supprimer le sinus carré. Pour cela on utilise la relation :
![]()
Et on obtient :
![]()
Comme on a :
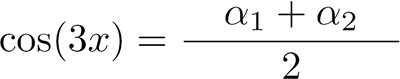
On en déduit la forme décomposée de cos (3x) :
![]()
Formules générales de la décomposition :
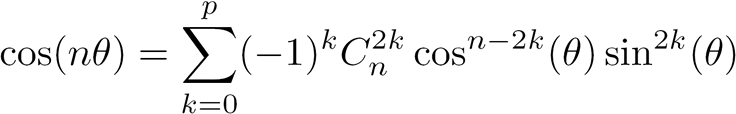
avec p la partie entière de n / 2
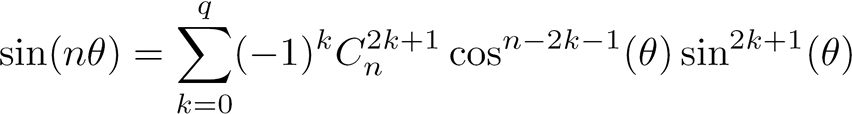
avec q la partie entière de (n - 1) / 2
Rappel :
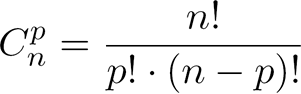
Incroyable mais vrai !
Pour enfin tout comprendre sur l'intégration par changement de variable !
Retrouver toutes les techniques de recherche rapide des racines d'un polynome de degré quelconque
Comment calculer cos(pi/n) en utilisant le triangle de Pascal ?
Calcul de la valeur exacte de COS (pi / 5)
Nous allons, dans ce paragraphe, démontrer la relation suivante :
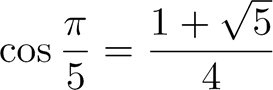
Commençons
par décomposer |
en utilisant la technique de décomposition |
. On obtient :
![]()
Posons |
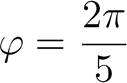 |
et |
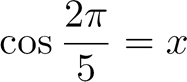 |
On obtient :
![]()
Appelons P(x) le polynôme suivant :
![]()
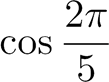 |
est une racine de P(x) : |
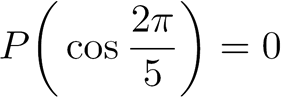
Comme la somme des coefficients de P(x) est nulle (16-20+5-1=0), 1 est une racine évidente de P(x) :
![]()
On peut donc factoriser P(x) par x - 1 :
![]()
Identification des coefficients du polynôme du 4ème degré :
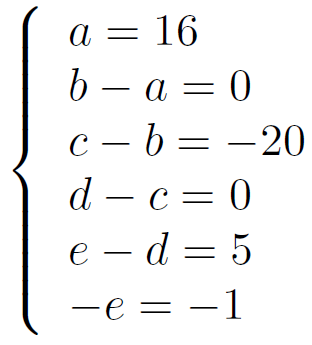
On en déduit les valeus suivantes pour les 5 coefficients :
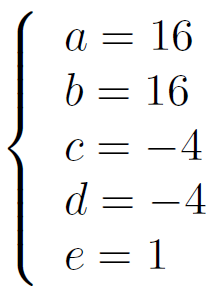
Et le polynôme P(x) s'écrit alors :
![]()
Or, le polynôme |
est le carré
d'un polynôme de degré 2 : |
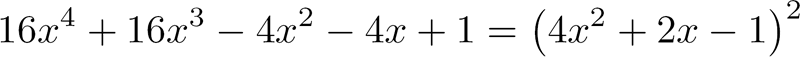
Ce qui nous donne pour P(x) :
![]()
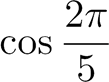 |
est donc
une racine de |
Résolvons l'équation algébrique du second degré suivante, en appelant x1 et x2 les deux racines:
![]()
Calcul du discriminent Delta :
![]()
Les racines x1 et x2 sont :
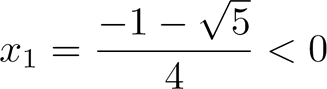

Comme |
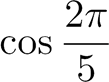 |
est positif,
on a |
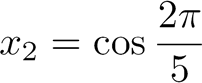 |
Soit :
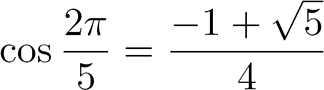
Il faut
maintenant retrouver |
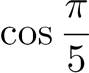 |
alors qu'on
connaît |
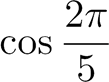 |
Grâce
à la technique de décomposition,
on peut démontrer que |
On peut en déduire la relation suivante :
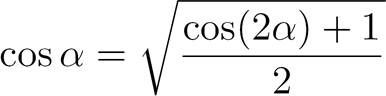
Appliquons
cette relation pour trouver |
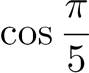 |
à
partir de |
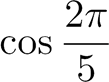 |
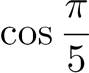 |
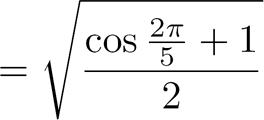 |
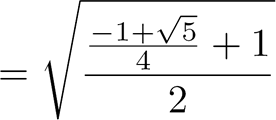 |
|
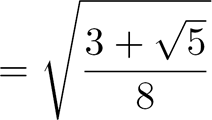 |
|
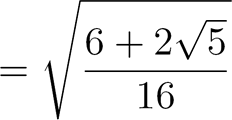 |
|
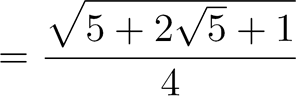 |
|
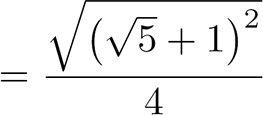 |
|
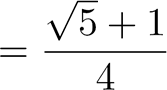 |
Et Voilà, c'est fini ! Voici le résultat final, que nous venons de démontrer :
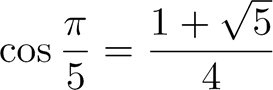
Remarque :
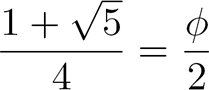
Où |
est le
nombre d'or : |
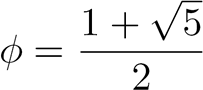
Il existe
donc une relation directe entre le nombre |
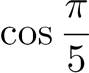 |
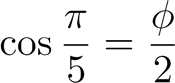
Incroyable mais vrai !
Pour enfin tout comprendre sur l'intégration par changement de variable !
Retrouver toutes les techniques de recherche rapide des racines d'un polynome de degré quelconque
Comment calculer cos(pi/n) en utilisant le triangle de Pascal ?