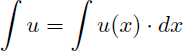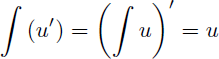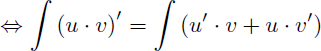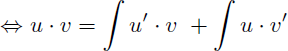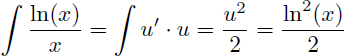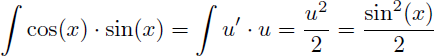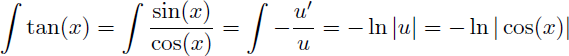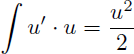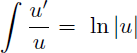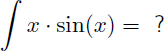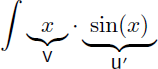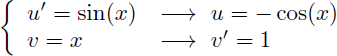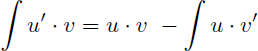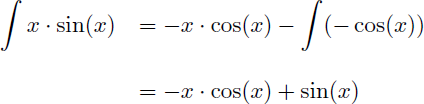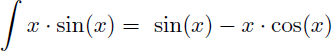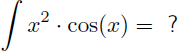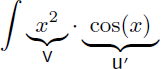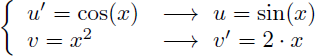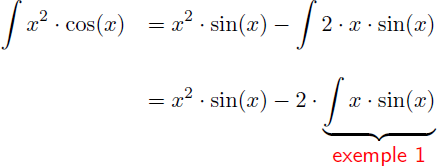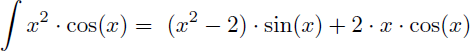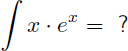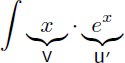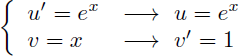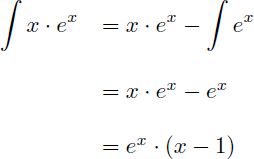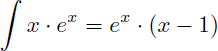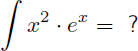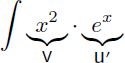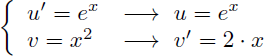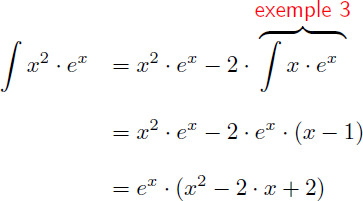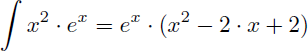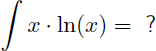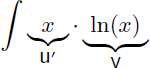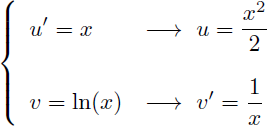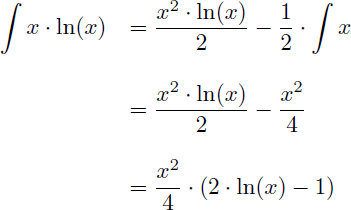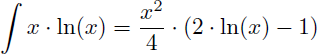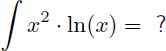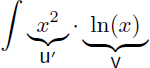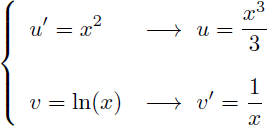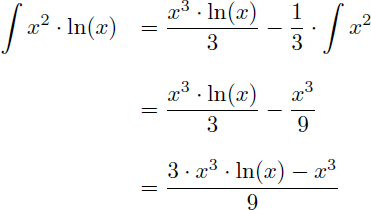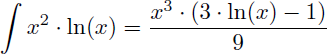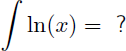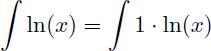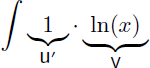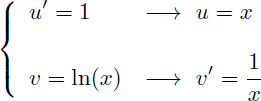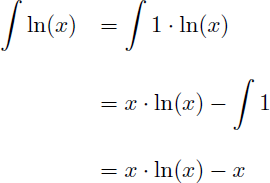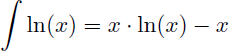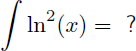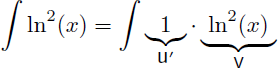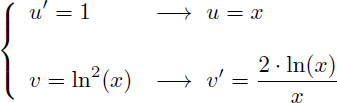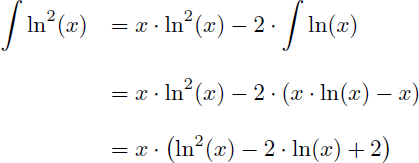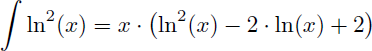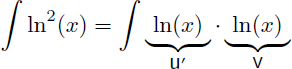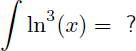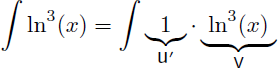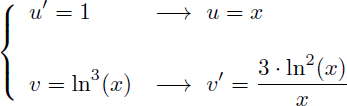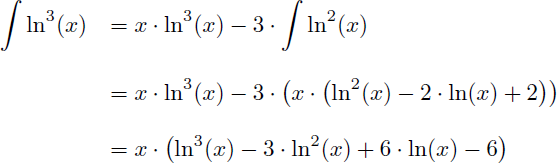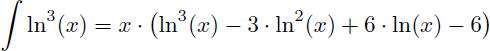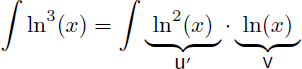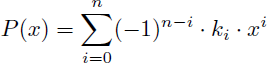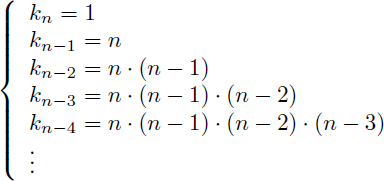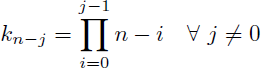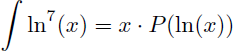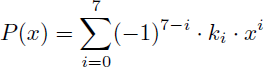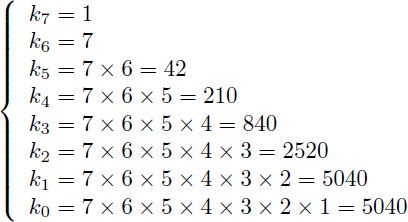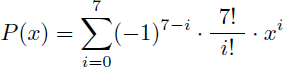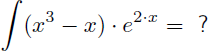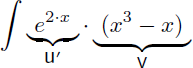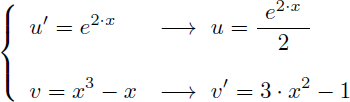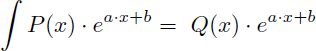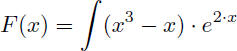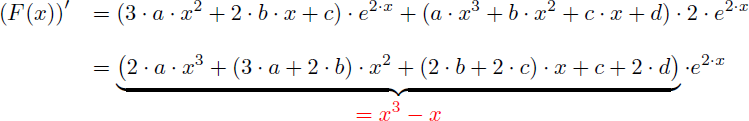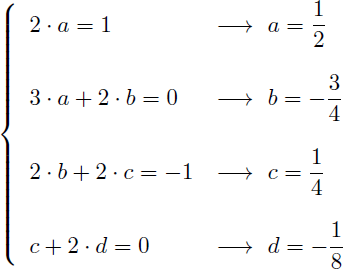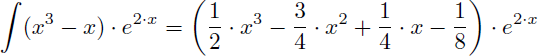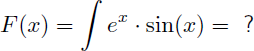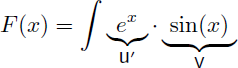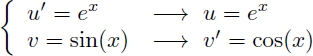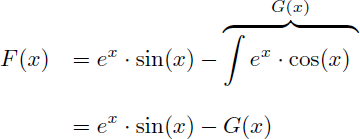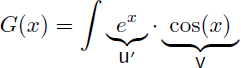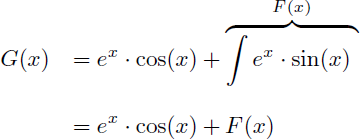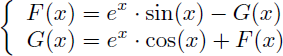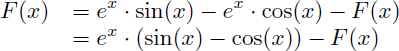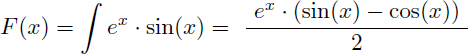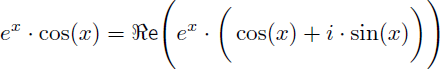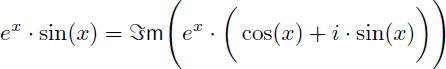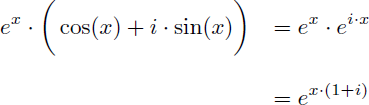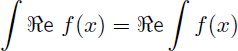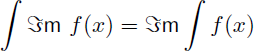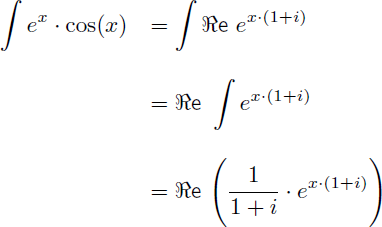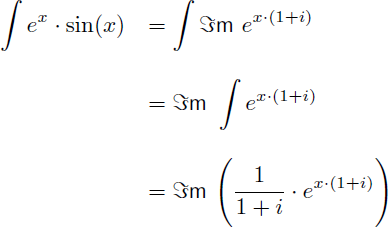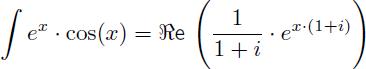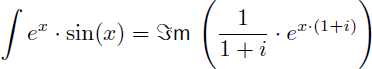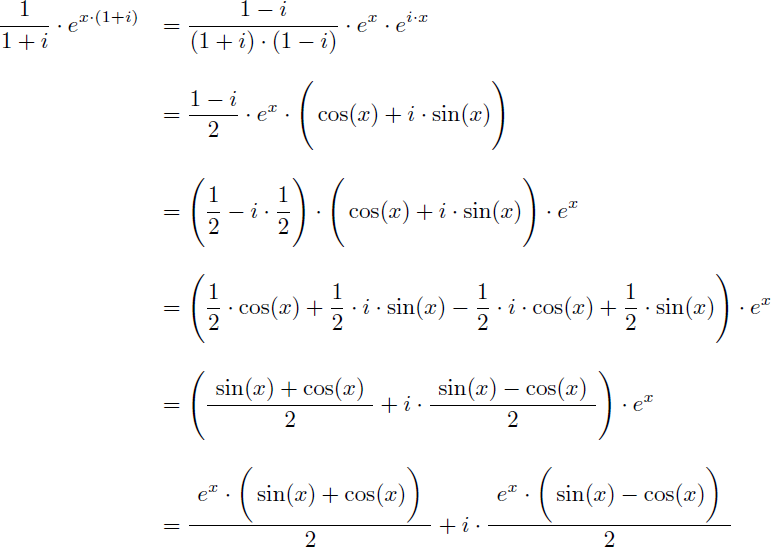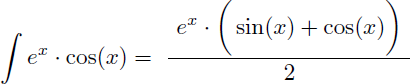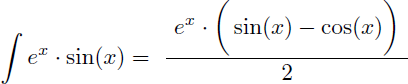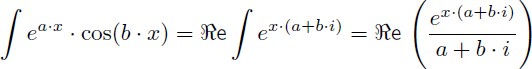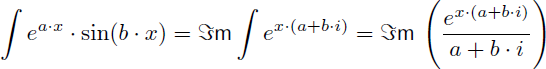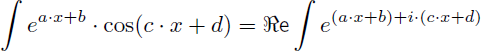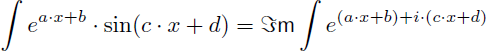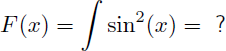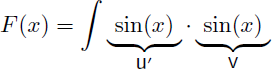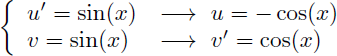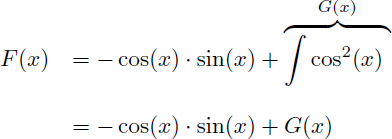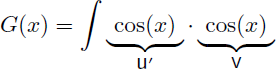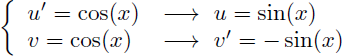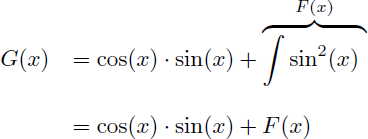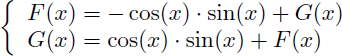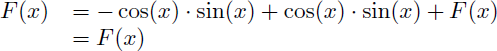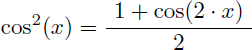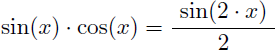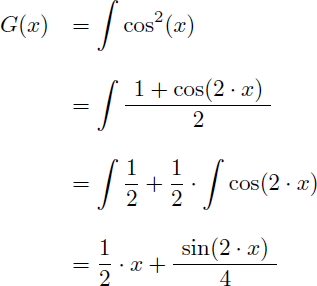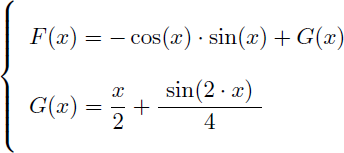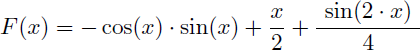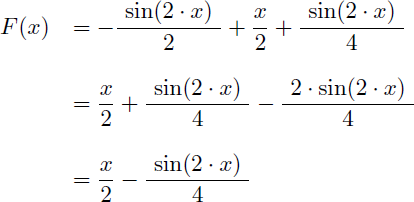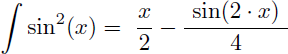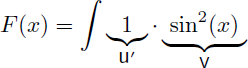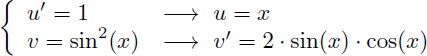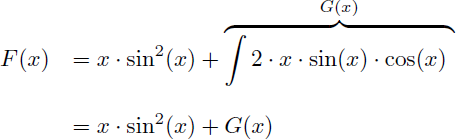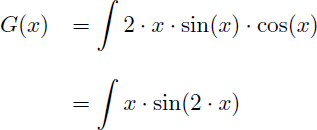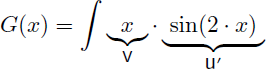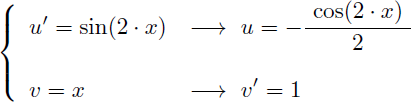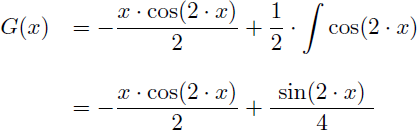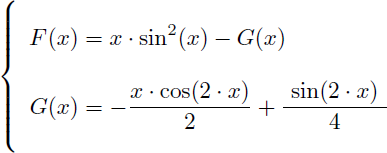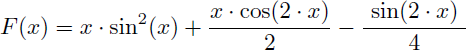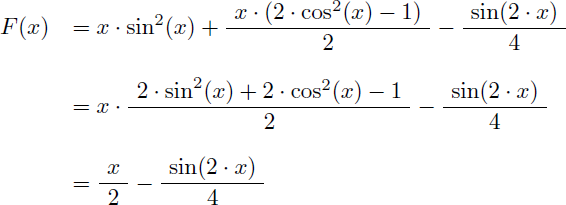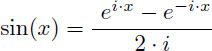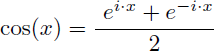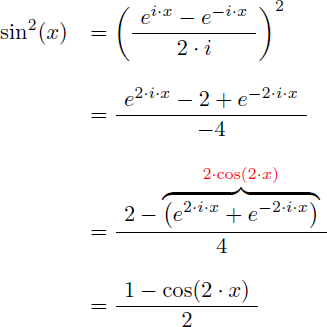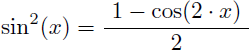L'intégration par parties

 Introduction 

Cet article explique le mécanisme de l'intégration par parties à travers différents exemples concrets, détaillés et commentés dans le but de trouver la primitive d'une fonction. Lors de l'illustration du calcul de primitives, de nombreuses astuces seront données pour aller plus vite, certaines astuces permettant même d'éviter parfois l'intégration par parties.

Comme pour tous les articles mathématiques du site Gecif.net la vulgarisation mathématique permet ici d'expliquer avec des mots et des notions simples (de niveau BAC) des résultats qui demandent en principe un niveau bien supérieur.

Le calcul de dérivées doit être parfaitement connu avant de vouloir effectuer une recherche de primitives par intégration par parties.

 

Retour en haut de la page

 Notions de base 

Règles d'écriture adoptées ici

Nous ne traiterons ici que les intégrales indéfinies, c'est-à-dire le calcul de primitives sans valeurs numériques. De plus, afin de se concentrer sur le mécanisme de l'intégration par parties :

• l'ensemble de définition des fonctions ne sera pas précisé
• la continuité des fonctions ne sera ni testée ni rappelée
• le symbole dx ne sera pas écrit dans les intégrales (car ici il ne sert à rien)
• il n'y a pas de bornes d'intégration
• les fonctions u(x) et v(x) seront notées simplement u et v
• la constante k permettant d'obtenir l'ensemble des primitives ne sera pas indiquée : on donne ici une seule primitive

L'écriture volontairement simplifiée employée sur cette page utilisera les symboles suivants :

• le symbole "prime" représente "la fonction dérivée, par rapport à x, de" :

• et le symbole "intégrale" (ou symbole "somme") représente "la fonction primitive, par rapport à x, de" :

Ces deux abréviations remplacent donc les écritures complètes suivantes :

On sait déjà que :

Remarque : u est la primitive de u'

En dépit d'une écriture simplifiée concernant les fonctions, les dérivées et les primitives, l'opérateur "multiplication" sera lui systématiquement représenté par le symbole "point" dans toutes les expressions mathématiques sur cette page, sans jamais être sous-entendu, même devant une parenthèse. Par exemple :

• 2x sera toujours écrit 2.x
• a(b+1) sera toujours écrit a.(b+1)
• ax²+bx+c sera toujours écrit a.x²+b.x+c
• etc.

Enfin, pour clore ce paragraphe sur les règles d'écriture utilisées sur cette page, les fonctions "partie réelle d'un nombre complexe" et "partie imaginaire d'un nombre complexe" seront représentées respectivement par les symboles suivants :

 

Démonstration de la formule de l'intégration par parties

En partant de la dérivée du produit de deux fonctions :

On en déduit la formule de l'intégration par parties :

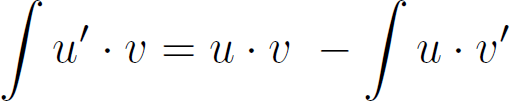
Remarque : cette formule de l'intégration par parties n'est que la conséquence de la dérivée du produit de deux fonctions et peut donc se retrouver facilement si on sait que (u.v)'=u'.v+u.v'

 

Principe et condition d'utilisation de l'intégration par parties

Le "mécanisme" de l'intégration par parties consiste à écrire la fonction dont on cherche la primitive sous la forme d'un produit u'.v puis d'en déduire u et v' avant d'appliquer la formule de l'intégration par parties.

L'intégration par parties est particulièrement intéressante pour calculer les primitives des fonctions de la forme :

Dans tous les cas le choix de u' et de v dans le produit initial des deux fonctions se fera en remarquant les règles suivantes :

• la dérivée de xⁿ simplifie l'expression car elle diminue l'exposant
• la primitive de xⁿ complique l'expression car elle augmente l'exposant
• la dérivée de ln(x) qui est 1/x simplifie l'expression car elle diminue l'exposant
• la primitive de ln(x) complique l'expression (et n'est pas forcément connue)
• les primitives de sin(x), cos(x) et e^x ne complique pas la fonction initiale

En résumé, dans la plupart des cas il faudra de préférence :

• dériver xⁿ et ln(x)
• intégrer sin(x), cos(x) et e^x

Remarque : sachant que la primitive de u'.u est u²/2 et que la primitive de u'/u est ln |u| la recherche des primitives suivantes ne nécessite pas d'intégration par parties :

Il en est de même pour toutes les fonctions de la forme u'.u ou u'/u

 

A retenir avant de commencer une intégration par parties :

 

Rappel : il faut ajouter une constante k aux résultats indiqués afin d'obtenir toutes les primitives de la fonction. Dans tous les exemples de cette page on ne donne en résultat qu'une seule primitive.

La suite de cette page expose 12 exemples détaillés et commentés de calcul de primitive par intégration par parties.

Retour en haut de la page

Exemple 1 

Voyons dans ce premier exemple comment trouver la primitive de x.sin(x) en utilisant l'intégrtation par parties :

Rappel : la primitive de sin(x) est -cos(x)

Sans hésitation on choisit v=x et u'=sin(x) afin que le calcul de v' simplifie l'expression, alors que la primitive de sin(x) ne change en rien la complexité :

On en déduit alors u et v' :

Remarques :

• u est la primitive de u'
• v' est la dérivée de v

Appliquons la formule de l'intégration par parties qui est :

On en déduit que :

Conclusion : la primitive de x.sin(x) est sin(x)-x.cos(x) :

Rappel : il faut ajouter une constante k aux résultats indiqués afin d'obtenir toutes les primitives de la fonction. Dans tous les exemples de cette page on ne donne en résultat qu'une seule primitive.

Retour en haut de la page

Exemple 2

Nous recherchons maintenant la primitive de x².cos(x) :

Rappel : la primitive de cos(x) est sin(x)

Afin de dériver le polynôme en x et d'intégrer la fonction trigonométrique le choix de u' et de v est le suivant :

On en déduit alors u (la primitive de u') et v' (la dérivée de v) :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on en déduit que :

Dans ce résultat il nous faut calculer la primitive de x.sin(x) ce qui fait l'objet d'une nouvelle intégration par parties.

Comme nous l'avons vu à l'exemple 1 :

On en déduit donc la primitive de x².cos(x) :

Retour en haut de la page

 

Exemple 3

Voyons dans cet exemple comment trouver la primitive de x.e^x :

Rappel : la primitive de e^x est e^x

On choisit v=x afin que v' soit "plus simple" de v, et on choisit u'=e^x car sa primitive u n'est pas plus complexe :

On en déduit alors u (la primitive de u') et v' (la dérivée de v) :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

On en déduit la primitive de x.e^x :

A retenir : e^x est la seule fonction égale à sa primitive. La plupart des autres fonctions ont souvent une primitive "plus compliquée" que la fonction elle même. Lorsqu'il y a la fonction e^x dans une intégration par parties il faut l'intégrer puisque sa primitive est également e^x, c'est-à-dire qu'elle n'est pas "plus compliquée", ce qui est une chance. Chaque fois que cela sera possible on choisira donc u'=e^x.

Retour en haut de la page

 

Exemple 4

Nous recherchons maintenant la primitive de x².e^x :

Comme dans l'exemple 3 on intègre e^x et on dérive le polynôme en x :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

Lors du calcul de la primitive de x².e^x il nous faut calculer la primitive de x.e^x ce qui fait l'objet d'une nouvelle intégration par parties.

Comme nous l'avons vu à l'exemple 3 :

On en déduit la primitive de x².e^x :

Retour en haut de la page

 

Exemple 5

Voyons maintenant comment trouver la primitive de x.ln(x) :

Rappel : la dérivée de ln(x) est 1/x

En considérant que l'on ne connaît pas la primitive de ln(x) nous choisissons cette fois de dériver ln(x) et d'intégrer x. De plus la dérivée de ln(x) fait "baisser d'une unité l'exposant" de la primitive de x :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

On en déduit la primitive de x.ln(x) :

Retour en haut de la page

Exemple 6

Nous recherchons maintenant la primitive de x².ln(x) :

Rappel : la dérivée de ln(x) est 1/x

En considérant que l'on ne connaît pas la primitive de ln(x) nous choisissons de dériver ln(x) et d'intégrer x². De plus la dérivée de ln(x) "diminue d'un degré" la primitive de x² :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

On en déduit la primitive de x².ln(x) :

Retour en haut de la page

 

Exemple 7

Nous recherchons maintenant la primitive de ln(x) :

Mais comment calculer la primitive de ln(x) en utilisant l'intégration par parties alors que ln(x) n'est pas le produit de 2 fonctions ? L'astuce consiste tout simplement à écrire 1.ln(x) à la place de ln(x) : ainsi écrit nous avons bien un produit ! :-)

Et comme nous ne connaissons pas encore la primitive de ln(x) (puisqu'on la cherche ...) on intègre le 1 et on dérive ln(x) :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

On en déduit la primitive de ln(x) :

A retenir : si on sait dériver une fonction f(x) et que l'on sait calculer la primitive de x.f'(x) il est alors possible de trouver une primitive de f(x) en écrivant f(x)=1.f(x) dans une intégration par parties.

Retour en haut de la page

Exemple 8

Voyons dans cet exemple comment trouver la primitive de ln²(x) :

Comme pour l'exemple 7 l'astuce consiste à écrire 1.ln²(x) à la place de ln²(x) afin d'avoir un produit et de pouvoir appliquer une intégration par parties :

On a donc :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

Remarque : pour calculer la primitive de ln²(x) nous avons besoin de connaître la primitive de ln(x) qui a été trouvée à l'exemple 7 :

Le calcul de la primitive de ln²(x) nécessite donc 2 niveaux d'intégration par parties.

On en déduit la primitive de ln²(x) :

Remarque : comme nous connaissons la primitive de ln(x) on aurait pu aussi choisir u' et v comme ceci afin d'intégrer directement ln(x) dès le début :

Retour en haut de la page

Exemple 9

Deux techniques de calcul de primitive sont proposées ci-dessous pour cet exemple : >> avec intégration par parties en un premier temps >> sans intégration par parties en un second temps en utilisant une nouvelle méthode

Voyons dans cet exemple comment trouver la primitive de ln³(x) :

Comme pour l'exemple 8 l'astuce consiste à écrire 1.ln³(x) à la place de ln³(x) afin d'avoir un produit et de pouvoir appliquer une intégration par parties :

On a donc :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient :

Remarque : pour calculer la primitive de ln³(x) nous avons besoin de connaître la primitive de ln²(x) qui a été trouvée à l'exemple 8 :

Le calcul de la primitive de ln³(x) est donc une intégration par parties à 3 niveaux.

On en déduit la primitive de ln³(x) :

Remarque : comme nous connaissons la primitive de ln²(x) on aurait pu aussi choisir u' et v comme ceci afin d'intégrer directement ln²(x) dès le début :

Maintenant que vous avez compris et que vous connaissez les primitives de ln(x), ln²(x) et ln³(x) vous pouvez vous amuser à calculer le plus rapidement possible les primitives de ln⁴(x), ln⁵(x) et ln⁶(x) dont voici le résultat final :

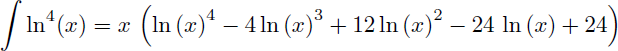
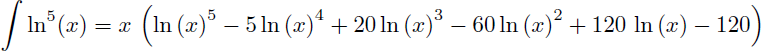
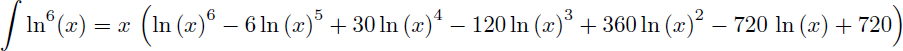
Remarques :

• Pour caluler la primitive de ln⁶(x) il faut utiliser la primitive de ln⁵(x) dans une intégration par parties
• Pour caluler la primitive de ln⁵(x) il faut utiliser la primitive de ln⁴(x) dans une intégration par parties
• Pour caluler la primitive de ln⁴(x) il faut utiliser la primitive de ln³(x) dans une intégration par parties
• Pour caluler la primitive de ln³(x) il faut utiliser la primitive de ln²(x) dans une intégration par parties
• Pour caluler la primitive de ln²(x) il faut utiliser la primitive de ln(x) dans une intégration par parties
• Pour caluler la primitive de ln(x) il faut faire une intégration par parties en posant ln(x)=1.ln(x)

Le calul de la primitive de lnⁿ(x) nécessite donc à première vue une intégration par parties à n niveaux.

Mais on peut aussi remarquer une régularité dans les coefficients des polynômes en ln(x) en observant les résultats précédents, comme expliqué dans le paragraphe suivant.

Calcul de la primitive de lnⁿ(x) sans intégration par parties :

La primitive de lnⁿ(x) sera toujours de la forme x.P(ln(x)) où P(x) est un polynôme de degré n.

En appelant k₀ à k_n les valeurs absolues des coefficents du polynôme P(x) on peut remarquer que :

En observant ci-dessus les primitives de ln²(x) à ln⁶(x) on peut remarquer que les valeurs absolues des coefficents k_n à k₀ du polynôme sont :

Et de manière générale les valeurs absolues des coefficients autre que celui du monôme de plus haut degré (qui est k_n=1) sont :

En utilisant la fonction factorielle l'expression de tous les coefficients s'écrit (y compris celui du monôme de plus haut degré) :

Rappel : 0!=1

Exemple d'application : vous recherchez la primitive de ln⁷(x) ? Rien de plus simple ! Nous n'allons pas faire une intégration par parties à 7 niveaux ! La primitive de ln⁷(x) s'écrit x.P(ln(x)) :

Avec P(x) un polynôme de degré 7 dont les signes des coefficients sont alternés :

Soit en abrégé :

Avec :

Les valeurs absolues des coefficents k₇ à k₀ du polynôme P(x) sont :

En alternant le signe des coefficients k₇ à k₀ on obtient le polynôme P(x) :

En résumé ce polynôme P(x) n'est autre que :

Et on peut donc en déduire, sans intégration par parties à 7 niveaux et sans connaître la primitive de ln⁶(x), que la primitive de ln⁷(x) est :

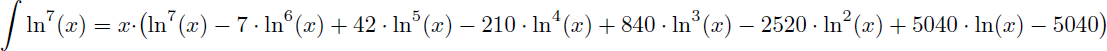
A retenir : en mathématiques l'observation et l'expérience peuvent souvent remplacer une technique purement mécanique, longue et fastidieuse. Cette remarque est particulièrement vraie en analyse dans le calcul intégral comme je viens de le démontrer en trouvant, de manière improvisée et par simple observation, la primitive de lnⁿ(x) sans faire d'intégration par parties :

Retour en haut de la page

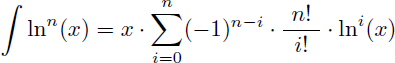
Exemple 10

Voyons dans cet exemple comment trouver la primitive de (x³-x).e^2.x :

On pourrait calculer la primitive de (x³-x).e^2.x en s'inspirant de l'exemple 4 :

Ce qui donnerait pour l'intégration par parties :

Mais de cette manière, pour calculer la primitive de (x³-x).e^2.x il nous faudra calculer la primitive de (3.x²-1).e^2.x pendant l'intégration par parties : la primitive de (x³-x).e^2.x nécessiterait ainsi une intégration par parties à 3 niveaux, ce qui est possible mais évitable comme nous allons le voir.

Pour éviter cette intégration par parties à 3 niveaux il faut savoir que la primitive d'une fonction de la forme :

avec P(x) un polynôme de degré n, est toujours de la forme :

avec Q(x) un polynôme de même degré que P(x).

On peut donc écrire et retenir que :

La recherche de la primitive peut alors se faire par simple identification des coefficients entre deux polynômes de degré n au lieu d'effectuer une succession de n intégrations par parties.

Illustrons cette technique en calculant la primitive F(x) de (x³-x).e^2.x :

La primitive F(x) recherchée est de la forme suivante :

Dérivons F(x) qui est le produit de deux fonctions : (u.v)'=u'.v+u.v' :

Or la dérivée de F(x) est (x³-x).e^2.x puisque F(x) est la primitive de (x³-x).e^2.x (ben quoi, c'est clair, non ?? :-)).

Identifions les coefficients des deux polynômes de degré 3 :

On en déduit la primitive de (x³-x).e^2.x :

A retenir : cette méthode par identification des coefficients de deux polynômes de degré 3 a remplacé une intégration par parties à 3 niveaux (c'est-à-dire 3 intégrations par parties successives). La primitive de P(x).e^a.x+b s'obtient donc sans faire d'intégration par parties.

Retour en haut de la page

Exemple 11

Cet exemple montre comment trouver la primitive de sin(x).e^x que nous appellerons F(x) :

La question qui se pose alors est de savoir s'il faut intégrer sin(x) ou e^x sachant que dans les deux cas la primitive est de même complexité. En réalité les deux cas sont possibles et aucun n'est plus avantageux que l'autre. Nous allons ici intégrer e^x et dériver sin(x)  puisque nous avons vu à l'exemple 3 qu'il fallait intégrer e^x chaque fois que cela était possible :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient une expression de F(x) en fonction d'une nouvelle primitive G(x) :

Pour déterminer F(x) il nous faut calculer la nouvelle primitive G(x), toujours en utilisant l'intégration par parties. Comme G(x) est de la même forme que F(x) nous intégrons à nouveau e^x :

On a donc :

En appliquant la formule de l'intégration par parties on obtient cette fois une expression de G(x) en fonction de F(x) :

Les deux intégrations par parties nous donnent donc un petit système à deux équations, et deux inconnues F(x) et G(x) :

En résolvant par substitution ce système simple on trouve pour F(x) :

On en déduit alors la primitive F(x) de sin(x).e^x :

A retenir : pour ne pas "tourner en rond" et sortir de cette intégration par parties à 2 niveaux nous avons intégré 2 fois e^x (dans F(x) et dans G(x)). La procédure reste la même pour calculer la primitive de cos(x). e^x par intégration par parties.

Mais il existe une autre solution pour calculer les primitives de cos(x).e^x et de sin(x).e^x en utilisant cette fois les nombres complexes et sans utiliser d'intégration par parties comme nous allons le voir maintenant.

 

Calcul des primitives de sin(x).e^x et de cos(x).e^x sans faire d'intégration par parties :

cos(x).e^x est la partie réelle du nombre complexe e^x.(cos(x)+i.sin(x)) :

sin(x).e^x est la partie imaginaire du même nombre complexe e^x.(cos(x)+i.sin(x)) :

Rappel de la forme exponentielle du nombre complexe de module 1 et d'argument x (formule d'Euler) :

Donc le nombre complexe e^x.(cos(x)+i.sin(x)) s'écrit :

Rappel : la primitive de e^a.x est e^a.x/a (avec a constant, réel ou complexe).

Sachant que la partie réelle d'une intégrale est égale à l'intégrale de la partie réelle, et que la partie imaginaire d'une intégrale est égale à l'intégrale de la partie imaginaire on peut écrire :

On en déduit que la primitive de cos(x).e^x est :

Et on en déduit aussi que la primitive de sin(x).e^x est :

Les primitives recherchées sont donc simplement les parties réelle et imaginaire d'un nombre complexe :

La recherche des primitives de cos(x).e^x et de sin(x).e^x revient donc à rechercher la partie réelle et la partie imaginaire de ce nombre complexe.

Il faut maintenant décomposer en partie réelle et partie imaginaire le nombre complexe suivant, ce qui revient à passer de sa forme exponentielle à sa forme algébrique :

La décomposition en partie réelle et partie imaginaire se fait comme ceci :

Et comme on a :

On en déduit les primitives de cos(x).e^x et de sin(x).e^x :

Rappel : la primitive de e^z.x est e^z.x/z (avec z complexe).

En ajoutant un coefficient à x on peut déduire des résultats précédents les relations suivantes (avec a et b deux réels constants) :

Et de manière générale on retiendra de cet exemple 11 que (avec a, b, c et d quatre réels constants) :

A retenir : l'utilisation des nombres complexes permet de trouver les primitives de e^a.x+b.cos(c.x+d) et de e^a.x+b.sin(c.x+d) sans faire d'intégration par parties.

Retour en haut de la page

 

Exemple 12

Dans ce dernier exemple on va "essayer" (sans garantie d'efficacité en un premier temps) de trouver la primitive F(x) de sin²(x) par intégration par parties. Nous verrons en un second temps comment éviter l'intégration par parties pour ce genre de primitives.

Essayons de trouver la primitive F(x) de sin²(x) par intégration par parties, en procédant comme pour l'exemple 11 :

sin²(x) n'étant ni de la forme u'.u ni de la forme u'/u il n'y a pas de méthode directe donnant sa primitive. Nous allons voir ici ce que donne l'intégration par parties.

Il faut exprimer sin²(x) sous la forme u'.v. Nous avons le choix entre u'=sin(x) et v=sin(x) ou bien u'=1 et v=sin²(x).

Posons par exemple u'=sin(x) et v=sin(x) :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient une expression de F(x) en fonction d'une nouvelle primitive G(x) :

Pour déterminer F(x) il nous faut calculer la nouvelle primitive G(x), toujours en utilisant l'intégration par parties :

On a donc :

En appliquant la formule de l'intégration par parties on est content puisqu'on obtient cette fois une expression de G(x) en fonction de F(x) :

On pense alors qu'on est sur le bonne voie puisqu'on a trouvé F(x) en fonction de G(x) et G(x) en fonction de F(x). :-)

Les deux intégrations par parties nous donnent donc un petit système à deux équations, et deux inconnues F(x) et G(x) :

Et là surprise, en résolvant par substitution ce système simple on trouve pour F(x) :

On obtient comme résultat F(x)=F(x) : ça nous avance vachement beaucoup ... :-(

En fait les deux intégrations par parties nous ont donné exactement le même renseignement : G(x)-F(x)=cos(x).sin(x). Nous avons donc bien deux inconnues F(x) et G(x) mais une seule équation. Il ne nous est donc pas possible de trouver les valeurs de F(x) et de G(x).

En réalité cet exemple montre que l'intégration par parties ne permet pas d'obtenir directement la primitive de sin²(x) et montre surtout pourquoi l'intégration par parties ne fonctionne pas dans ce cas. :-)

Mais le choix de prendre u'=sin(x) et v=sin(x) était-il la seule solution au départ ? Non, on aurait pu aussi prendre u'=1 et v=sin²(x) mais est-ce que ça aurait marché ? La réponse est non car le blocage ne vient pas du choix initial de u' et v : tant qu'on ne transforme pas cos²(x) ou sin(x).cos(x) l'intégration par parties ne donnera pas la primitive de sin²(x).

Si malgré tout on veut vraiment calculer la primitive de sin²(x) en utilisant l'intégration par parties (et sans linéariser), les formules de trigonométrie à connaître et qui vont nous sauver sont les suivantes :

On en déduit alors les formules de transformation qui vont débloquer la situation :

Quand et comment utiliser ces formules de transformation afin que l'intégration par parties de sin²(x) aboutisse ?

• SOLUTION 1 : si au départ de l'intégration par parties on fait le choix de prendre u'=sin(x) et v=sin(x) il faut alors remplacer cos²(x) par son équivalent en fonction de cos(2.x) dans l'intégrale intermédiaire G(x)
• SOLUTION 2 : si au départ de l'intégration par parties on fait le choix de prendre u'=1 et v=sin²(x) il faut alors remplacer sin(x).cos(x) par son équivalent en fonction de sin(2.x) dans l'intégrale intermédiaire G(x)

 

Voyons maintenant dans le détail comment retrouver la primitive de sin²(x) par intégration par parties en utilisant les deux solutions différentes.

 

Démonstration complète avec la SOLUTION 1 :

On recherche F(x) la primitive de sin²(x) :

Il faut exprimer sin²(x) sous la forme u'.v. Dans cette SOLUTION 1 on pose u'=sin(x) et v=sin(x) :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient une expression de F(x) en fonction d'une nouvelle primitive G(x) :

Pour déterminer F(x) il nous faut maintenant calculer la nouvelle primitive G(x).

Mais attention, avant de calculer la primitive G(x) il faut la transformer, sans quoi l'intégration par parties n'aboutirait à rien.

En utilisant la formule de transformation suivante :

On obtient pour G(x) :

En résumé on vient de trouver pour F(x) et G(x) :

On en déduit F(x) par substitution :

Il s'agit bien d'une primitive de sin²(x). Mais nous pouvons la simplifier en remplaçant sin(x).cos(x) par son équivalent en fonction de sin(2.x).

Sachant que :

On en déduit que :

Et nous obtenons (enfin) la primitive de sin²(x) grâce à l'intégration par parties :

Nous venons de démontrer le calcul de la primitive de sin²(x) par intégration par parties en utilisant une première solution. Voyons maintenant la seconde solution.

 

Démonstration complète avec la SOLUTION 2 :

On recherche F(x) la primitive de sin²(x) :

Il faut exprimer sin²(x) sous la forme u'.v. Dans cette SOLUTION 2 on pose cette fois u'=1 et v=sin²(x) :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient une expression de F(x) en fonction d'une nouvelle primitive G(x) :

Pour déterminer F(x) il nous faut calculer la nouvelle primitive G(x).

Mais attention, avant de calculer la primitive G(x) il faut la transformer, sans quoi l'intégration par parties n'aboutirait à rien.

En utilisant la formule de transformation suivante :

On obtient pour G(x) :

La primitive G(x) va maintenant être caculée par une seconde intégrations par parties.

Il faut exprimer G(x) sous la forme u'.v. On pose u'=sin(2.x) et v=x :

On en déduit u et v' :

Rappel de la formule de l'intégration par parties :

En appliquant la formule de l'intégration par parties on obtient pour G(x) :

En résumé on vient de trouver pour F(x) et G(x) :

On en déduit F(x) par substitution :

Il s'agit bien d'une primitive de sin²(x). Mais nous pouvons la simplifier en utilisant les deux relations suivantes.

Sachant que :

Et sachant que :

On en déduit que :

Et nous obtenons (enfin) la primitive de sin²(x) grâce à l'intégration par parties :

Nous venons de démontrer le calcul de la primitive de sin²(x) par intégration par parties en utilisant deux solutions différentes.

Comparaison des deux solutions nous ayant permis d'obtenir la primitive de sin²(x) par intégration par parties :

• dans la SOLUTION 1 le calcul de la primitive G(x) est direct, sans effectuer une seconde intégration par parties
• dans la SOLUTION 2 le calcul de la primitive G(x) nécessite une seconde intégration par parties
• la SOLUTION 1 est donc une intégration par parties à 1 niveau alors que la SOLUTION 2 est une intégration par parties à 2 niveaux. Cela s'explique car dans la SOLUTION 2 nous n'avons rien intégrer au premier niveau en choisissant u'=1 : le travail reste à faire lors du calcul de G(x)
• on peut donc remarquer que plus u' est comliqué dès le départ, plus le travail sera avancé à l'issue de la première intégration par parties
• en revanche, si on choisit u' trop simple (par exemple en prenant u'=1) on peut avoir besoin d'effectuer une seconde intégration par parties pour "finir le travail"
• la SOLUTION 1 est donc préférable et plus efficace que la SOLUTION 2 puisqu'elle utilise directement la primitive de sin(x) que nous connaissons dès la première intégration par parties
• dans les deux solutions les deux formules de tansformation on été utilisées pour simplifier les expressions trigonométriques : cos(2.x) et sin(2.x)
• l'intégration par parties à 2 niveaux ne nous dispense donc pas de connaître les relations trigonométriques, ce qui confirme que la SOLUTION 2 a peu d'intérêt ...
• dans la SOLUTION 2, faute de ne pas avoir intégrer sin(x) à la première intégration par parties, on doit intégrer sin(2.x) en guise de punition à la seconde intégration par parties ... :-(
• la SOLUTION 2 présente tout de même l'avantage d'éliminer astucieusement sin²(x) et cos²(x) en utilisant simplement la formule sin²(x)+cos²(x)=1 et sans utiliser de formule de linéarisation, contrairement à la SOLUTION 1 qui utilise directement la linéarisation de cos²(x)

Dans les deux démonstrations précédentes (la SOLUTION 1 et la SOLUTION 2) je n'ai volontairement pas parler de linéarisation ni de formule d'Euler, en me limitant à de simples "formules de transformation" résultant des relations élémentaires de trigonométrie : on a seulement utilisé les développements de sin(2.x) et cos(2.x). Ces deux démonstrations ont pour but de montrer qu'on peut obtenir la primitive de sin²(x) par intégration par parties sans "parler" de linéarisation ni de formule d'Euler (même si c'est long et fastidieux ...). En réalité l'emploi des "formules de transformation" suivantes constituait (sans le dire) la linéarisation qui est indispensable pour intégrer sin²(x) :

Mais dans la pratique le plus simple pour obtenir la primitive de sin²(x) est de linéariser directement la fonction en utilisant la formule d'Euler puis de calculer la primitive de la forme linéarisée sans utiliser l'intégration par parties.

Linéariser sinⁿ(x) ou cosⁿ(x) consiste à les exprimer en fonction de cos(n.x) et de sin (n.x), ce qui permet de calculer facilement les primitives de sinⁿ(x) et de cosⁿ(x).

 

Calcul de la primitive de sin²(x) en linéarisant et sans faire d'intégration par parties :

Pour linéariser sin²(x) on part des formules d'Euler :

Sachant que :

On en déduit que :

Après linéarisation de sin²(x) on obtient donc l'expression suivante pour sin²(x) :

En calculant la primitive de la forme linéarisée de sin²(x) on obtient directement et sans intégration par parties :

La procédure reste similaire pour calculer les primitives de sinⁿ(x) et de cosⁿ(x) qui sont par exemple utilisées dans les intégrales de Wallis.

A retenir : l'intégration par parties ne permet pas de calculer facilement les primitives de sinⁿ(x) ou de cosⁿ(x). Dans la pratique pour obtenir la primitive de sinⁿ(x), de cosⁿ(x), ou de sinⁿ(x).cos^m(x) il faut linéariser les expressions en utilisant notamment la formule d'Euler, puis calculer directement la primitive de la forme linéarisée sans faire d'intégration par parties.

 

Pour aller plus loin :

Cliquez ici pour obtenir toutes les techniques de linéarisation de sinⁿ(x) et de cosⁿ(x)

Cliquez ici pour obtenir les techniques d'intégration par changement de variable

 

Retour en haut de la page