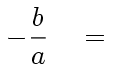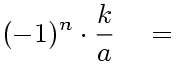Calcul instantané des racines d'un polynôme de degré quelconque
Petite question préliminaire :
Pouvez-vous donner de tête et immédiatement les solutions de l'équation du 3ème degré suivante ?
![]()
Non ? C'est tout à fait normal pour l'instant. Mais sachez qu'après avoir lu cet article, vous serez capable de résoudre de tête et en quelques secondes une telle équation, et même des équations algébriques plus complexes. Vous avez du mal à y croire ? Alors je vous invite à lire attentivement l'article ci-dessous : vous allez être surpris de vos possibilités intellectuelles et surtout des techniques de calcul instantané dévoilées ici.
Comme pour tous les articles mathématiques du site Gecif.net la vulgarisation mathématique permet ici d'expliquer avec des mots et des notions simples (de niveau BAC) des résultats qui demandent en principe un niveau bien supérieur.
Introduction
En mathématiques, pour trouver les racines d'un polynôme il existe principalement 4 méthodes :
- la méthode complète qui consiste à exprimer les valeurs exactes des racines sous forme de fractions et radicaux en passant (notamment) par le discriminant delta
- la méthode par transformation qui consiste à réécrire le polynôme sous une autre forme (factorisation si on connaît déjà une racine, forme canonique, changement de variable, etc.)
- la méthode par analyse qui donne une valeur approchée des racines en analysant la courbe représentative de la fonction polynôme
- la méthode alternative, moins connue et utilisée dans certains tours de magie par les calculateurs prodiges, qui permet de donner rapidement les valeurs exactes des racines, quel que soit le degré du polynome, à partir du moment où ce dernier répond à certains critères particuliers
Nous allons voir ici seulement la méthode alternative, ou plutôt les méthodes alternatives, qui permettent, dans certains cas particuliers de trouver instantanément les valeurs exactes des racines d'un polynôme de degré quelconque sans passer par la méthode complète.
Lorsqu'on parle de recherche les racines d'un polynôme on pense tout de suite à Delta, c'est-à-dire à la méthode complète. Pourtant, les méthodes alternatives présentées ici, permettent dans la plupart des cas d'obtenir bien plus rapidement les racines, y compris dans des polynôme de degré supérieur à 2, tout en démontrant que l'on maîtrise les propriétés des polynômes.
Définitions et conventions utilisées
L'écriture générale d'un polynome est :
![]()
Détails des différents éléments de cette expression :
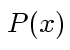 |
est la fonction
polynôme |
x |
est la variable
de la fonction P(x) |
n |
est le degré
du polynôme |
est le monôme
de degré n |
|
est le monôme
de degré n-1 |
|
est le monôme
de degré n-2 |
|
a |
est le coefficient
du monôme de degré n |
b |
est le coefficient
du monôme de degré n-1 |
c |
est le coefficient
du monôme de degré n-2 |
k |
est le coefficient
du monôme de degré 0 : il s'agit du terme constant du polynôme
(appelé aussi "la constante") |
Un polynôme de degré n possède n+1 monômes.
| Par exemple, le polynôme | de degré 2 possède 3 monômes. |
Dans tout ce qui suit lorsque je parlerai de "polynôme", je parle en fait de la fonction polynôme et non d'un polynome en tant qu'objet mathématique (qui aurait pu être vu comme un élément pris dans un espace vectoriel). Cette remarque s'adresse en particulier aux mathématiciens puristes, s'il y en a parmi vous.
Rappel concernant la propriété fondamentale des polynômes
On appelle "racine" d'un polynôme, la valeur (ou les valeurs) de x qui annule la fonction polynôme P(x). Un polynôme de degré n possède exactement n racines, qui peuvent être soit réelles, soit complexes.
| Les racines sont ici notées |
| Si les racines d'un polynôme | 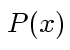 |
de degré n sont |
| alors | 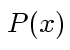 |
peut toujours se factoriser de la manière suivante : |
![]()
Application imédiate : vous recherchez un polynôme de degré 3 ayant comme racines 1, 5, et 7 ? Votre polynôme s'écrit donc :
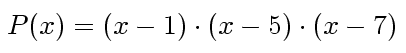
Après développement de cette forme factorisée vous obtenez le polynôme de degré 3 suivant qui a bien 1, 5, et 7 comme racines :
![]()
Autre exemple, avec des racines complexes cette fois : on désire trouver un polynôme de degré 4 ayant pour racines 3+2i , 3-2i , -5 , et 8
La forme factorisée du polynôme est :
![]()
Après développement de cette forme factorisée, vous obtenez le polynôme de degré 4 suivant, qui a bien 3+2i , 3-2i , -5 , et 8 comme racines :
![]()
| On remarque donc qu'un polynôme | 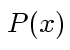 |
ayant pour racines |
peut toujours se factoriser de la manière suivante, et ce quelle que soit la nature (réelles ou complexes) des racines :
![]()
Cette remarque est en contradiction avec ce qu'on a dû vous apprendre au lycée, puisqu'on a vous a appris que la factorisation d'un polynôme n'est possible que dans le cas où les racines sont réelles (delta positif, pour un polynôme de degré 2).
Pourtant, la factorisation est aussi possible dans le cas où les racines sont complexes, à condition de garder en mémoires les remarques suivantes :
- un polynôme de degré impair a toujours au moins 1 racines réelles : les autres sont soit réelles, soit complexes conjuguées deux à deux
- un polynôme de degrés pair peut avoir soit des racines réelles, soit des racines complexes conjuguées deux à deux
Par exemple pour un polynôme de degré 3, il y a forcément 1 racine réelle. Les deux autres racines sont soit réelles toutes les deux, soit complexes conjuguées.
Un polynôme de degré 4 peut avoir :
- soit 4 racines réelles
- soit 2 racines réelles et 2 racines complexes, les deux racines complexes étant conjuguées
- soit 4 racines complexes, conjuguées deux à deux (par exemple 3+2i et 3-2i et puis 7+5i et 7-5i)
Mais il est impossible d'obtenir un polynôme de degré 2 à coefficient réels dont les racines sont 3+2i et 7+5i (ces racines n'étant pas des complexes conjugués).
J'appelle propriété fondamentale des polynômes le fait qu'un polynôme puisse toujours s'écrire sous la forme factorisée suivante, faisant apparaîte chacune de ses racines :
![]()
Conséquence de la propriété fondamentale des polynômes
Voici, sans la démontrer, la conséquence de la propriété fondamentale des polynômes. Cette conséquence, qui s'écrit sous forme de 2 affirmations, est la base des méthodes de recherche alternatives des racines :
Quel que soit le degré n d'un polynôme, et quelle que soit la nature de ses racines (réelles ou complexes), on aura toujours :
|
Dans ces deux expressions :
n |
est le degré
du polynôme |
a |
est le coefficient
du monôme de degré n |
b |
est le coefficient
du monôme de degré n-1 |
k |
est le coefficient
du monôme de degré 0 : il s'agit du terme constant du polynôme
(appelé aussi "la constante") |
Cette remarque fondamentale nous donne un lien direct entre la somme ou le produit des racines, et certains des coefficients du polynômes.
Dernières définitions avant de commencer ...
Avant d'attaquer la recherche de racines dans des cas concrets, voici quelques informations complémentaires, ainsi que les conditions dans lesquelles nous allons nous placer pour appliquer les méthodes alternatives.
Polynôme unitaire
On appelle polynôme unitaire un polynôme dont le coefficient du monôme de plus haut degré vaut 1.
Les polynômes suivants sont des polynômes unitaires (car a = 1) :
![]()
![]()
![]()
Comme le coefficent du monôme de plus haut degré vaut 1 la factorisation d'un polynôme unitaire est la suivante :
![]()
Equation algébrique
On appelle équation algébrique une équation de la forme P(x)=0 où P est un polynôme.
Exemple d'équations algébriques :
![]()
![]()
Remarque : toute équation algébrique peut se mettre sous la forme P(x) = 0, où P(x) est un polynôme unitaire. Il suffit pour cela de diviser les deux membres de l'équation algébrique par le coefficient du monôme de plus haut degré (le coefficient a). Exemple :
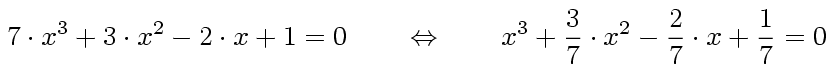
Trouver les solutions d'une équation algébrique revient donc à déterminer les racines d'un polynôme unitaire.
Nombres algébriques et nombres transcendants
Le nombre x est un nombre algébrique s'il existe un polynôme P à coefficients rationnels tel que P(x)=0. Autrement dit, un nombre (réel ou complexe) qui est une solution d'une équation algébrique est un nombre algébrique : toute racine d'un polynôme à coefficients rationnels est un nombre algébrique. Mais un nombre algébrique n'est pas forcément réel. Par exemple le nombre complexe i est algébrique puis qu'il est la solution d'une équation algébrique à coefficents rationnels.
Un nombre algébrique est donc un nombre "solution d'une équation algébrique", et peut être soit réel soit complexe.
Nous pouvons constater que tout nombre entier ou rationnel est un nombre algébrique (car le nombre rationnel p/q sera toujours solution de l'équation algébrique q.x-p=0), mais que certains nombres réels ne sont pas algébriques (c'est le cas par exemple du nombre Pi=3,14159265358979...).
Un nombre (réel ou complexe) qui n'est pas algébrique est appelé un nombre transcendant.
Un nombre transcendant est donc un nombre "non-algébrique", et peut être soit réel soit complexe.
Conditions d'application des méthodes alternatives de recherche des racines d'un polynôme
Dans tout ce qui suit nous ne considèrerons que les polynômes répondant aux conditions suivantes :
- le degré du polynôme est quelconque
- les racines du polynôme sont toutes des nombre entiers relatifs (donc non complexes)
- le polynôme est unitaire : le coefficient a du monôme de plus haut degré vaut 1
Dans ces conditions, puisque le coefficient a=1, la conséquence de la propriété fondamentale des polynômes s'écrit :
la somme de toutes les racines = - b
|
Et maintenant, appliquons tout ça dans des exemples concrets ... C'est parti !
Recherche des racines dans un polynôme de degré quelconque, à l'aide de la méthode alternative
Exemple 1 :
![]()
Le degré du polynôme est pair : la constante 21 est donc égale au produit des 2 racines.
21 = 3x7 : les racines sont 3 et 7 ! !
Comment ça c'est trop simple ? En effet, c'est plus simple que de passer par Delta ... La résolution de l'équation se résume ici à une simple décomposotion en facteurs premiers afin de trouver 2 entiers dont le produit vaut 21.
Exemple 2 :
![]()
Cette fois on a :
![]()
Il faut donc trouver 2 nombres dont le produit est égal à -10
Il y a 2 solutions :
![]()
![]()
ce que j'écrirai désormais sous la forme :
![]()
Mais on sait que la somme des deux racines vaut -b, c'est-à-dire -3
On en déduit que les racines sont 2 et -5
Exemple 3 :
Le degré du polynôme est impair, et k = - 42. Le produit des racines vaut - k.
On recherche donc 3 nombres entiers dont le produit vaut 42.
![]()
Remarque : on a aussi 42 = 1x6x7
Mais comme la somme des racines doit être égale à 12, il n'y a qu'une seule solution : les racines sont 2, 3 et 7.
Comment ça c'est magique ? En effet, résoudre de tête en moins de 10 secondes une équation du troisième degré est à la hauteur de ce qu'un calculateur prodige est en mesure de faire (et encore ...). On continue !
Exemple 4 :
![]()
Le degré du polynôme est impair, et k = 42. Le produit des racines vaut - k.
On recherche ici 3 nombres entiers dont le produit vaut -42.
![]()
La somme des racines est égale à 6 : comment obtenir 6 en additionnant 3 nombres parmi les nombres 2, -2, 3, -3, 7, et -7 ?
La réponse est 6 = 2 - 3 + 7
Les racines sont donc 2, -3 et 7.
Cas des racines multiples :
![]()
Le degré du polynôme est impair, et k = - 8. Le produit des racines vaut - k.
![]()
On en déduit que 2 est une racine multiple d'ordre 3. En clair, les racines sont 2, 2, et 2 (3 fois le même nombre, mais il y a bien 3 racines). On constate que la somme des 3 racines est bien égale à - b = 6. Enfin, dans le cas de racines multiples, la forme factorisée du polynôme peut s'écrire de la manière suivante :
![]()
Ne pas oublier que 1 et k sont aussi des diviseurs de k :
![]()
Le degré du polynôme est pair, et k = - 10. Le produit des racines vaut k.
![]()
mais ni 2 ni -2 ni 5 ni -5 n'est racine du polynôme
En fait, on peut aussi écrire -10 de la manière suivante :
![]()
De manière générale, on pourra écrire :
![]()
ce qui veut dire que l'ensemble des diviseurs de - 10 est :
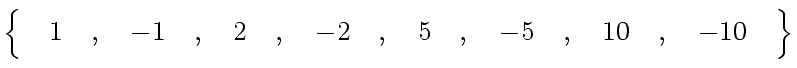
Parmi ces 8 diviseurs de - 10, on recherche 2 nombres dont la somme est égale à - 9
Les racines sont donc 1 et - 10
A retenir : Le coefficient k du monôme de degré 0 est un multiple de toutes les racines : cela ne signifie pas que les racines sont forcément des nombres premiers issue de la décomposotion en facteurs premiers de k
|
Il faut aussi savoir détecter le cas où les racines ne sont pas entières :
![]()
Le degré du polynôme est pair, et k = 6. Le produit des racines vaut k.
Nous recherchons donc deux nombres dont le produit vaut 6 et dont la somme vaut 8 :
![]()
Après test, on constate qu'aucun des diviseurs de 6 (2, -2, 3, -3, 1, -1, 6, et -6) n'est racine du polynôme. De plus il est impossible d'obtenir 8 en additionnant 2 de ces diviseurs (sauf 2+6 mais le produit ne fait plus 6). On en conclus que les racines de ce polynôme ne sont pas entières, et la méthode alternative s'arrête là. Les racines sont soit réelles, soit complexes, et il faudra utiliser la méthode complète (avec le discriminant Delta) pour en déterminer les valeurs.
Lien entre le signe des racines et le signe des coefficients
Dans un polynôme unitaire à racines entières les racines peuvent être toutes de même signe ou de signes différents. En observant le signe des coefficients du polynôme nous pouvons en déduires des informations importantes qui nous permettent d'accélérer encore plus la recherche des racines. Voici ces informations :
|
Appliquons ces remarques pour trouver les valeurs exactes des racines entières de polynômes de degré 3 et 4, à travers les 10 exemples suivants :
Exemple 1 :
![]()
![]() comme les coefficients sont tous positifs, on en déduit que les racines
sont toutes négatives
comme les coefficients sont tous positifs, on en déduit que les racines
sont toutes négatives
![]() 935 = 5 x 11 x 17 et la somme des racines est - 33
935 = 5 x 11 x 17 et la somme des racines est - 33
![]() les racines sont - 5 - 11 et - 17
les racines sont - 5 - 11 et - 17
Exemple 2 :
![]()
![]() comme le signe des coefficients est alternatif (positif négatif positif
négatif), on en déduit que les racines sont toutes positives
comme le signe des coefficients est alternatif (positif négatif positif
négatif), on en déduit que les racines sont toutes positives
![]() 2639 = 7 x 13 x 29 et la somme des racines est 49
2639 = 7 x 13 x 29 et la somme des racines est 49
![]() les racines sont 7, 13 et 29
les racines sont 7, 13 et 29
Dans les deux exemples précédents, la recherche des racines des polynômes de degré 3 se résume en une simple décomposition en facteurs premiers de la constante k du polynôme.
Exemple 3 :
![]()
![]() cette fois le signe des coefficients n'est pas régulier : on en déduit
qu'il y a à la fois des racines positives et des racines négatives
cette fois le signe des coefficients n'est pas régulier : on en déduit
qu'il y a à la fois des racines positives et des racines négatives
![]() 8601 = 3 x 47 x 61 et la somme des racines est - 11
8601 = 3 x 47 x 61 et la somme des racines est - 11
![]() - 11 = 3 + 47 - 61
- 11 = 3 + 47 - 61
![]() les racines sont 3, 47 et - 61
les racines sont 3, 47 et - 61
Exemple 4 :
![]()
![]() les racines ne sont pas toutes du même signe
les racines ne sont pas toutes du même signe
![]() 8601 = 3 x 47 x 61 et la somme des racines est - 17
8601 = 3 x 47 x 61 et la somme des racines est - 17
![]() - 17 = 47 - 61 - 3
- 17 = 47 - 61 - 3
![]() les racines sont 47, - 61 et - 3
les racines sont 47, - 61 et - 3
Exemple 5 :
![]()
![]() les signes des coefficients sont alternatifs, donc toutes les racines sont positives
les signes des coefficients sont alternatifs, donc toutes les racines sont positives
![]() mais cette fois le produit des racines est un nombre premier : le produit des
3 racines vaut 13
mais cette fois le produit des racines est un nombre premier : le produit des
3 racines vaut 13
![]() la somme des 3 racines est 15
la somme des 3 racines est 15
![]() les racines sont 13, 1 et 1
les racines sont 13, 1 et 1
![]() 13 est une racine d'ordre 1, et 1 est une racine multiple d'ordre
2
13 est une racine d'ordre 1, et 1 est une racine multiple d'ordre
2
Exemple 6 :
![]()
![]() les signes des coefficients sont alternatifs, donc toutes les racines sont positives
les signes des coefficients sont alternatifs, donc toutes les racines sont positives
![]() 384 = 3 x 2^7
384 = 3 x 2^7
![]() avec la décomposition en facteurs premier 3 x 2^7 il est possible
de composer 16 nombres différents, qui sont 1 2 3 4 6 8 12 16 24 32
48 64 96 128 192 et 384
avec la décomposition en facteurs premier 3 x 2^7 il est possible
de composer 16 nombres différents, qui sont 1 2 3 4 6 8 12 16 24 32
48 64 96 128 192 et 384
![]() les racines entières font partie de ces 16 nombres (qui sont les diviseurs
de 384)
les racines entières font partie de ces 16 nombres (qui sont les diviseurs
de 384)
![]() la somme des racines est 20, et comme toutes les racines sont positives, on
peut déjà éliminer les nombres supérieurs à
20 dans la liste des 16 diviseurs de 384
la somme des racines est 20, et comme toutes les racines sont positives, on
peut déjà éliminer les nombres supérieurs à
20 dans la liste des 16 diviseurs de 384
![]() les racines sont 2 4 6 et 8
les racines sont 2 4 6 et 8
Exemple 7 :
![]()
![]() les signes des coefficients sont alternatifs, donc toutes les racines sont positives
les signes des coefficients sont alternatifs, donc toutes les racines sont positives
![]() 73728 = 3^2 x 2^13
73728 = 3^2 x 2^13
![]() avec la décomposition en facteurs premier 3^2 x 2^13 il est possible
de composer (2+1).(13+1)=42 nombres différents, qui sont les diviseurs
de 73728
avec la décomposition en facteurs premier 3^2 x 2^13 il est possible
de composer (2+1).(13+1)=42 nombres différents, qui sont les diviseurs
de 73728
![]() les 4 racines entières recherchées font partie des 42 diviseurs
de 73728
les 4 racines entières recherchées font partie des 42 diviseurs
de 73728
![]() comme la somme des racines est 153, et comme toutes les racines sont positives,
on peut déjà éliminer les nombres supérieurs à
153 dans la liste des 42 diviseurs de 73728
comme la somme des racines est 153, et comme toutes les racines sont positives,
on peut déjà éliminer les nombres supérieurs à
153 dans la liste des 42 diviseurs de 73728
![]() après avoir testé tous les diviseurs de 73728 inférieurs
à 153, on constate que les racines sont 1 24
32 et 96
après avoir testé tous les diviseurs de 73728 inférieurs
à 153, on constate que les racines sont 1 24
32 et 96
Dans ce dernier cas, la méthode alternative ne nous donne pas directement les racines, mais une liste de "racines candidates" qu'il nous faut tester une à une. Bien qu'il ne s'agisse pas d'une méthode directe, et que certains d'entre vous ont envis d'appeler ça du "système D" (et ça commence à en être), il faut tout de même remarquer ce qui est remarquable : cette méthode alternative nous a donné au final les valeurs exactes des solutions d'une équation algébrique de quatrième degré !
Au suivant !
Exemple 8 :
![]()
![]() cette fois la constante du polynôme vaut zéro
cette fois la constante du polynôme vaut zéro
![]() il y a donc une racine évidente : x=0
il y a donc une racine évidente : x=0
![]() comme zéro est une racine, on ne peut pas diviser par x pour diminuer
le degré de l'équation, mais en revenche on peut factoriser par
(x - 0) ce qui nous donne :
comme zéro est une racine, on ne peut pas diviser par x pour diminuer
le degré de l'équation, mais en revenche on peut factoriser par
(x - 0) ce qui nous donne :
![]()
Les deux autres racines (en plus de x=0) sont donc les racines du polynôme de degré 2 suivant :
![]()
![]() les 2 racines sont positives
les 2 racines sont positives
![]() leur produit vaut 6
leur produit vaut 6
![]() leur somme vaut 5
leur somme vaut 5
![]() les racines de ce polynôme de degré 2 sont 2 et 3
les racines de ce polynôme de degré 2 sont 2 et 3
![]() les 3 racines du polynôme de degré 3 de départ sont donc
: 0 2 et 3
les 3 racines du polynôme de degré 3 de départ sont donc
: 0 2 et 3
On continue ? Allons-y !
Exemple 9 :
![]()
![]() cette fois les 2 coefficients des monômes de plus faible degré
sont nuls
cette fois les 2 coefficients des monômes de plus faible degré
sont nuls
![]() zéro est donc une racine double
zéro est donc une racine double
![]() les 2 autres racines se trouvent dans les diviseurs du coefficient de x^2
les 2 autres racines se trouvent dans les diviseurs du coefficient de x^2
![]() 21 = 3 x 7
21 = 3 x 7
![]() les racines sont 0 0 3 et 7
les racines sont 0 0 3 et 7
Exemple 10 :
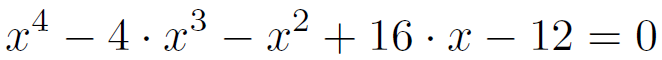
![]() il y a des racines positives et des racines négatives
il y a des racines positives et des racines négatives
![]() le produit des racines vaut - 12, qui se décompose de la manière
suivante :
le produit des racines vaut - 12, qui se décompose de la manière
suivante :
![]() - 12 = - (1 x 2 x 2 x 3)
- 12 = - (1 x 2 x 2 x 3)
![]() la sommes des racines vaut 4, que l'on compose à partir des diviseur
de - 12 de la manière suivante :
la sommes des racines vaut 4, que l'on compose à partir des diviseur
de - 12 de la manière suivante :
![]() 4 = 3 + 1 + 2 - 2
4 = 3 + 1 + 2 - 2
![]() les racines sont 3 1 2 et -
2
les racines sont 3 1 2 et -
2
Le polynôme de cet exemple 10 est en fait obtenu par le dévelopement de (x-3)(x-1)(x-2)(x+2), d'où les racines qui sont 3 1 2 et - 2
!! ATTENTION !!
L'analyse du polynôme suivant selon la même méthode donnerait le même résultat que l'exemple 10 :
![]()
Or les racines de ce polynômes ne sont pas 1, 2, 3 et -2. En effet ce polynôme n'est pas égal à (x-3)(x-1)(x-2)(x+2).
En réalité les racines de ce dernier polynôme ne sont pas entières, mais rien ne l'indique à première vue !
On ne le répètera jamais assez : la méthode alternative exposée sur cette page permet d'obtenir des "racines candidates" qui peuvent être les véritables racines du polynôme dans le cas d'un polynôme à racines entières, mais il faut dans tous les cas tester une à une les racines entières obtenues afin de vérifier si elle sont solution du polynôme.
A retenir : La méthode alternative exposée ici ne fonctionne que dans le cas où les racines sont entières. Mais rien n'indique à première vue si un polynôme possède seulement des racines entières. C'est la raison pour laquelle il faut absolument tester toutes les racines candidates avant d'affirmer qu'il s'agit des véritables solutions de l'équation algébrique.
|
L'objectif de cette page est de démontrer qu'il est possible de trouver les racines de polynôme de degré important là même où la plupart d'entre nous aurait envit de dire que c'est impossible. Un dernier exemple pour le prouver : quels sont les racines du polynôme de 9ème degré suivant :
![]()
Comme le signe des coefficients est alterné, on en déduit que les 9 racines sont toutes positives.
Le problème revient à rechercher 9 nombres entiers positifs dont la somme est 45 et dont le produit est 362880.
Vous avez trouvé ?
Réponse : les racines sont 1, 2, 3, 4, 5, 6, 7, 8 et 9.
Ce polynôme est en fait le résultat du développement de (x-9)*(x-8)*(x-7)*(x-6)*(x-5)*(x-4)*(x-3)*(x-2)*(x-1).
Les équations bicarrées
![]()
![]() cette fois 2 coefficients sont nuls (en x^3 et en x) mais ce ne sont pas les
coefficients des 2 monômes de degré le plus faible
cette fois 2 coefficients sont nuls (en x^3 et en x) mais ce ne sont pas les
coefficients des 2 monômes de degré le plus faible
![]() pour résoudre ce type d'équation algébrique (appellée équation bicarrée) on effectue le changement de
variable suivant :
pour résoudre ce type d'équation algébrique (appellée équation bicarrée) on effectue le changement de
variable suivant :
![]()
![]() l'équation devient alors un simple polynôme du second degré
en y :
l'équation devient alors un simple polynôme du second degré
en y :
![]()
![]() les 2 racines sont positives
les 2 racines sont positives
![]() le produit des racines vaut 225
le produit des racines vaut 225
![]() 225 = 25 x 9
225 = 25 x 9
![]() la somme des racines vaut 34
la somme des racines vaut 34
![]() les racines sont y=25 et y=9
les racines sont y=25 et y=9
Pour retrouver les 4 racines du polynôme en x de départ, on effectue le changement de variable inverse, sans oublier les valeurs négatives :
![]()
![]() les 4 solutions de l'équation bicarrée du quatrième degré
sont : 3 - 3 5 et -
5
les 4 solutions de l'équation bicarrée du quatrième degré
sont : 3 - 3 5 et -
5
![]() la résolution d'une équation bicarrée par changement de variable comme ici fait partie de ce qui a été appelé "les méthodes par transformation" dans l'introduction de cet article en haut de cette page
la résolution d'une équation bicarrée par changement de variable comme ici fait partie de ce qui a été appelé "les méthodes par transformation" dans l'introduction de cet article en haut de cette page