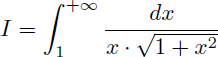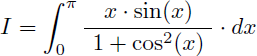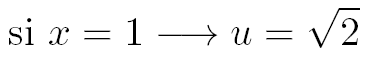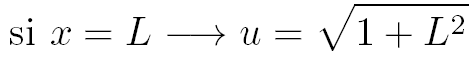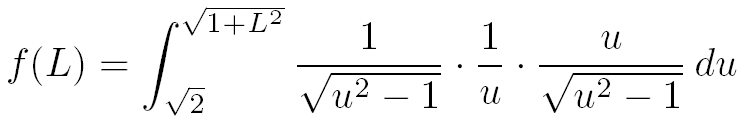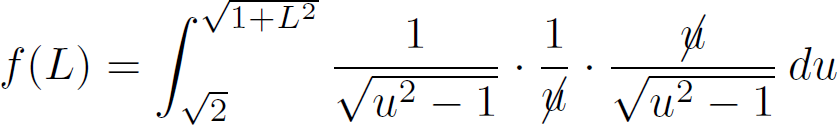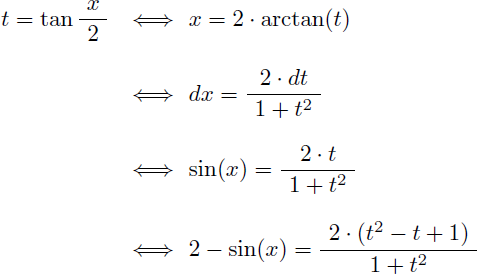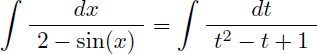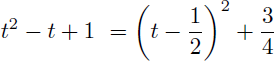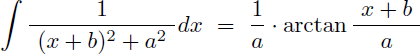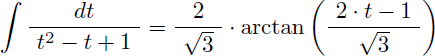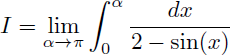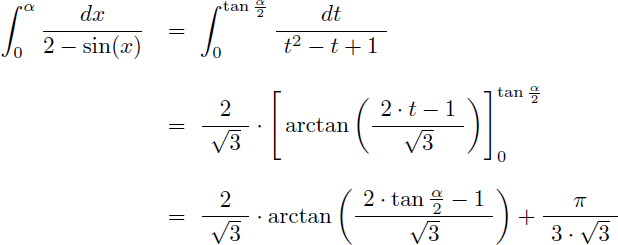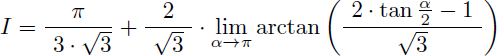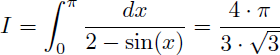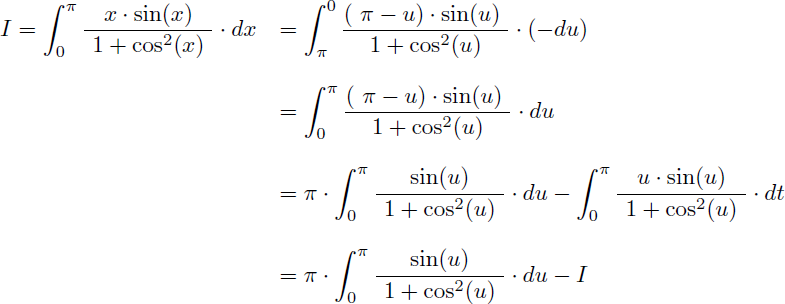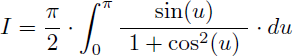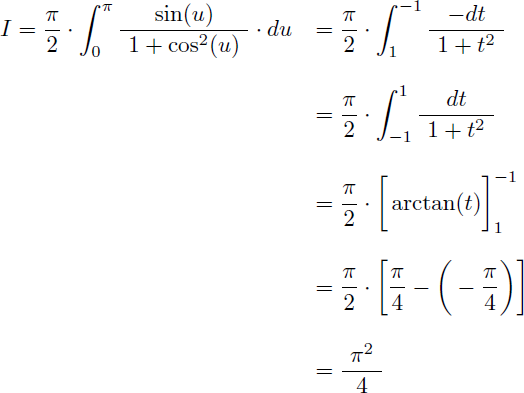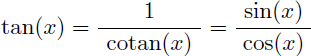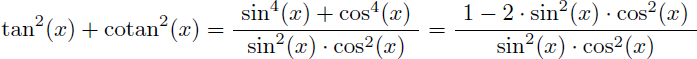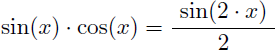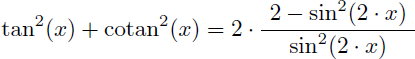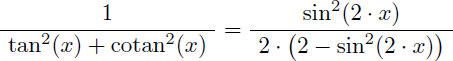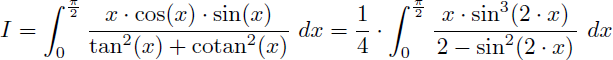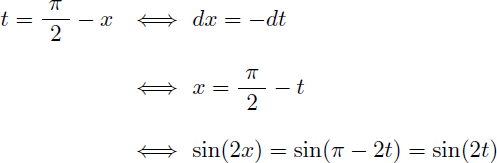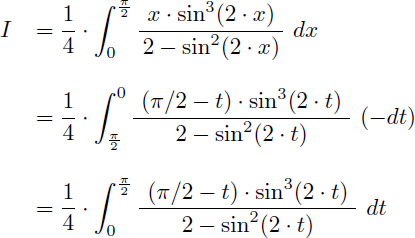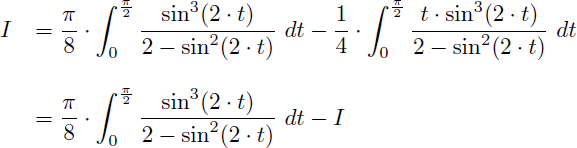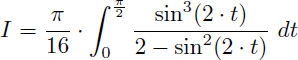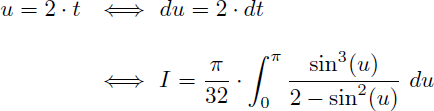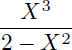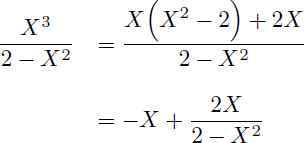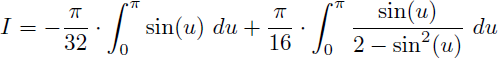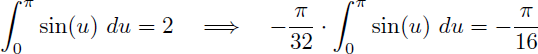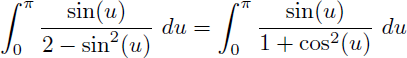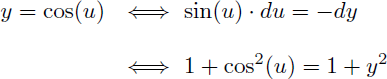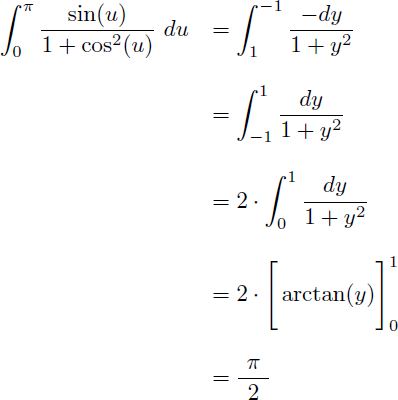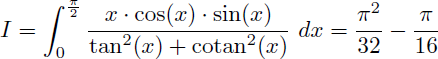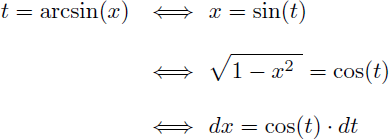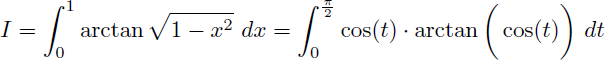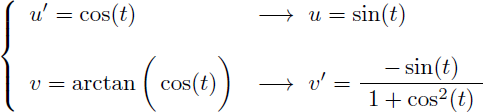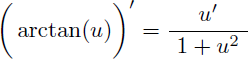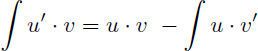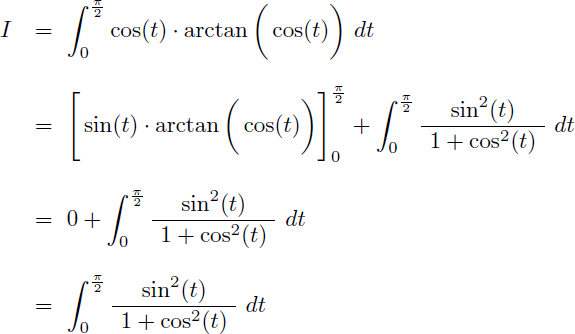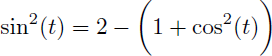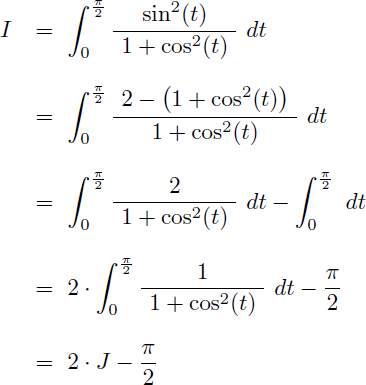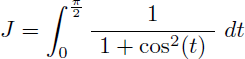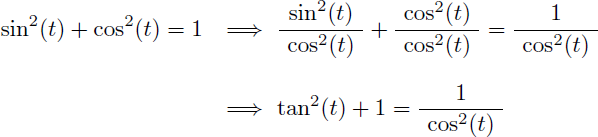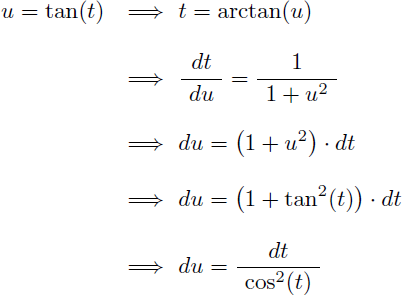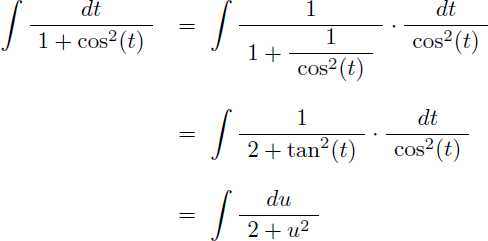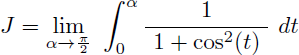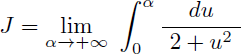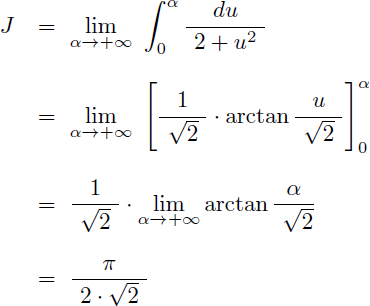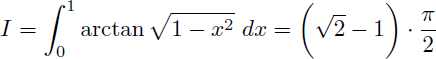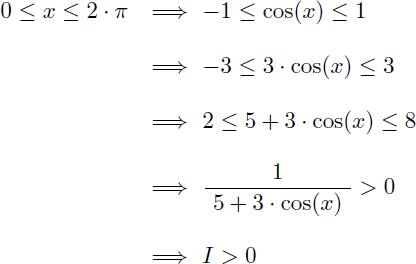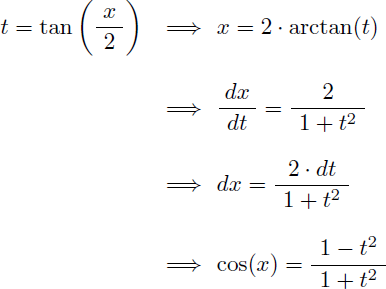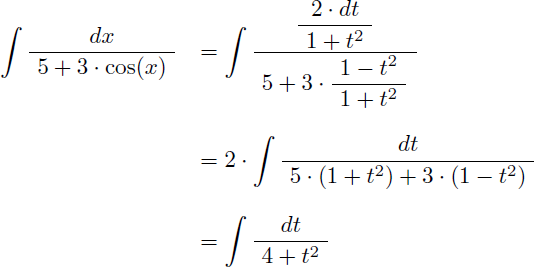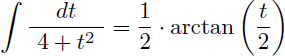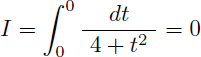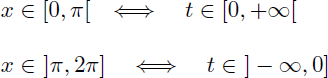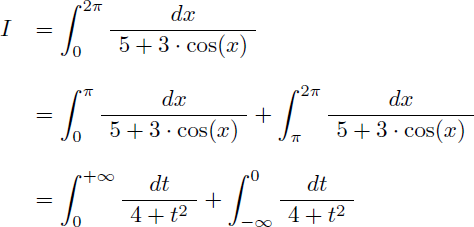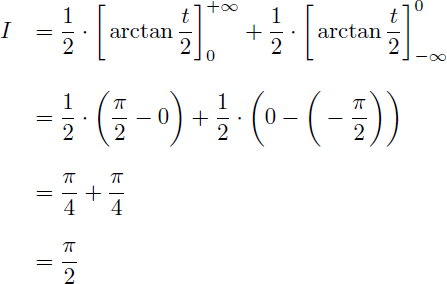Calcul d'une intégrale par changement de variable
Cet article explique en détail à travers plusieurs exemples comment calculer la valeur exacte d'une intégrale en utilisant notamment la technique du changement de variable. D'autres techniques mathématiques peuvent être utilisées dans les exemples ci-dessous en plus du changement de variable (intégration par parties, décomposition en éléments simples, calcul de limites, etc.).
Comme pour tous les articles mathématiques du site Gecif.net la vulgarisation mathématique permet ici d'expliquer avec des mots et des notions simples (de niveau BAC+1) des résultats qui demandent en principe un niveau bien supérieur.
Sommaire de cette page
|
|||||||||||||||||||||||||||
Le changement de variable |
Le changement de variable est une des techniques d'intégration les plus puissantes. Nous allons illustrer les possibilités du changement de variables à travers différents exemples concrets, divers et variés de calcul de primitives et d'intégrales définies.
Sans vouloir donner de recettes toutes faites ou de règles trop rigides, rappelons tout de même que le changement de variable est particulièrement efficace pour le calcul de la primitive d'une fonction composée (par exemple une primitive contenant une racine carrée).
Par exemple pour rechercher la primitive de la fonction composée f(g(x)) on pose souvent le changement de variable u=g(x), mais ce n'est pas systématique comme nous allons le voir dans les exemples ci-dessous.
De plus, même dans le cas du calcul de la primitive d'une fonction composée des alternatives au changement de variable existent.
Avec le changement de variable, l'élément différentiel de l'intégrale (le fameux "dx") va enfin prendre un rôle et une importance. En effet, dans toutes les autres techniques d'intégration le dx ne sert à rien et peut être totalement ignoré. Mais ici le changement de variable passe directement par cet élément dx, qui constitue le coeur de la transformation de l'intégrale.
Rappelons que le rapport du/dx représente la dérivée de la fonction u(x) par rapport à la variable x : du/dx=u'(x)
En multipliant les deux membres de l'égalité précédente par dx, on obtient aussi : du=u'(x).dx
Dans le changement de variable les éléments différentiels du et dx se manipulent comme toute autre variable réelle dans les équations (on peut les additionner, les multiplier, les diviser, les substituer, etc.). Et dans tous les cas il ne faut pas les perdre de vue !
Enfin il y a souvent plusieurs solutions possibles pour poser le changement de variable, les solutions exposées ici ne sont donc pas forcément uniques.
Passons à la pratique à travers plusieurs exemples de changement de variable diversifiés, clairs et détaillés.
EXEMPLE 1 |
Comment calculer la valeur exacte de l'intégrale I suivante ?
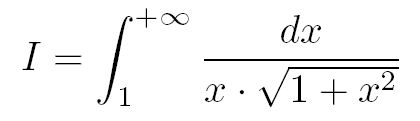
Solution détaillée :
La difficulté pour calculer l'intégrale I vient du fait que nous ne savons pas trouver une primitive de la fonction g(x) suivante :
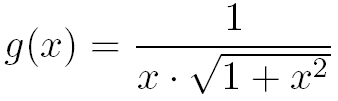
De plus l'intégrale I ne peut pas être calculée en utilisant l'intégration par parties, bien que g(x) soit le produit de deux fonctions et qu'il est possible de trouver la primitive de chacune de ces deux fonctions.
Sans savoir calculer une primitive de g(x) et sans utiliser l'intégration par parties nous allons tout de même réussir à calculer la valeur exacte de l'intégrale I. Nous utiliserons pour cela les principes mathématiques suivants :
- le changement de variable
- la décomposition en éléments simples
- le calcul de limite
L'intégrale I à calculer sera vue ici comme étant la limite à plus l'infini d'une fonction f(L) :
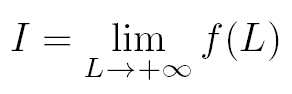
Avec pour la fonction f(L) :
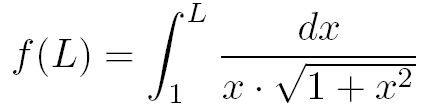
Voyons maintenant comment simplifier puis calculer la fonction f(L).
Etape 1 : le changement de variable
Pour faire "disparaître" la racine carrée de l'intégrale, effectuons le changement de variable suivant :
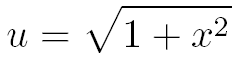
Avec ce changement de variable on a :
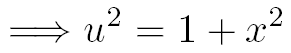
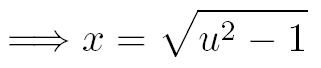
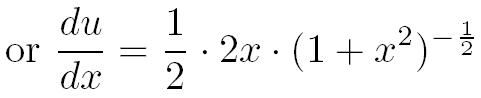
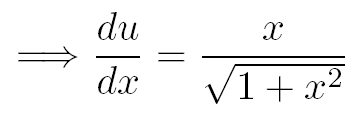
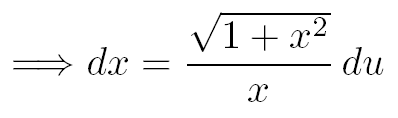
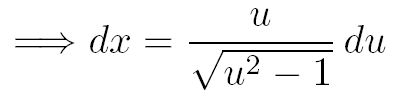
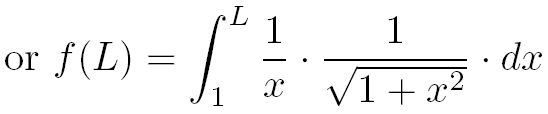
Grâce au changement de variable nous pouvons maintenant exprimer chacun des 3 termes de cette intégrale en fonction de u :
* |
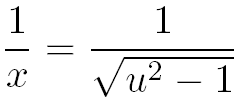 |
* |
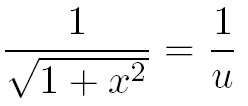 |
* |
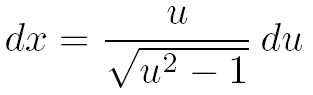 |
Le changement de variable nous permet alors d'écrire :
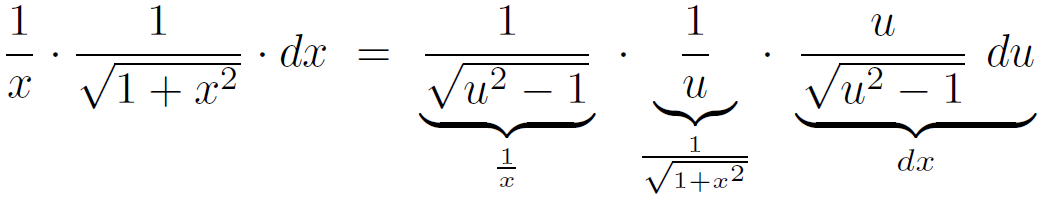
Calculons les nouvelles bornes de l'intégrale après le changement de variable :
En remplaçant les bornes de l'intégrale et après le changement de variable la fonction f(L) s'écrit :
On simplifie par u et on élève au carré la racine carrée :
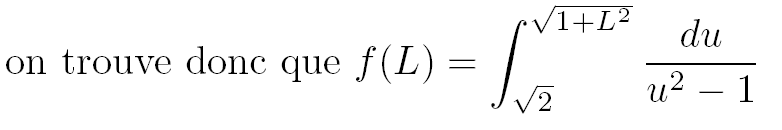
Grâce au changement de variable la fonction f(L) s'écrit finalement comme l'intégrale d'une fraction élémentaire (sans racines carrées), fraction qu'il est possible de décomposer en éléments simples.
Remarque : la racine carrée qui se trouvait au dénominateur de la fonction à intégrer (ce qui était un des éléments de blocage au début) se retrouve maintenant sur les bornes de l'intégrale suite au changement de variable (ce qui ne représente aucune difficulté puisque les bornes de l'intégrale ne sont que des valeurs constantes ou tendant vers l'infini).
Etape 2 : la décomposition en éléments simples
Décomposons maintenant en éléments simples la fraction suivante qui est présente dans f(L) :
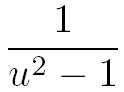
Le dénominateur de cette fraction est une différence de deux carrés, donc :
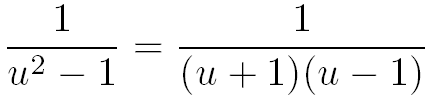
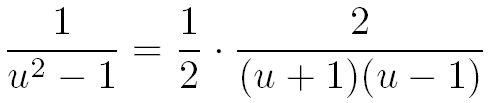
Sachant que (u+1)-(u-1)=2 on remplace le 2 du numérateur par (u+1)-(u-1) :
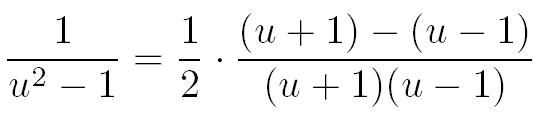
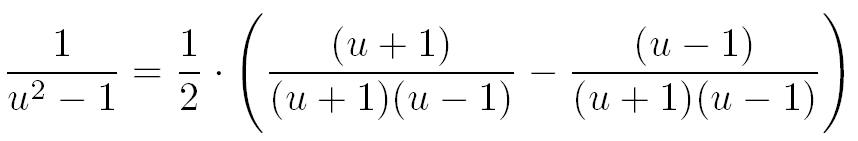
On simplifie les fractions :
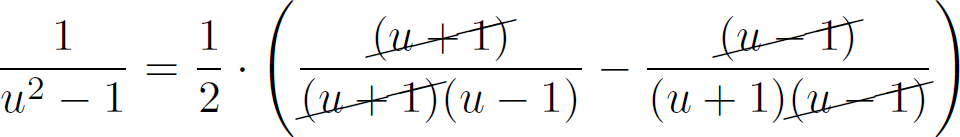
Et on obtient :
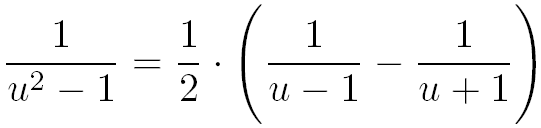
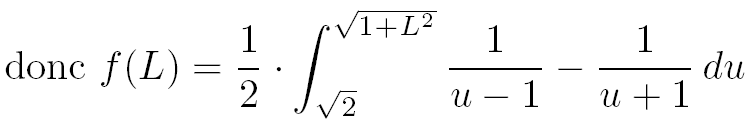
Grâce à la décomposition en éléments simples la fonction f(L) s'écrit comme l'intégrale de la différence de deux fonctions simples dont les primitives sont maintenant parfaitement connues :
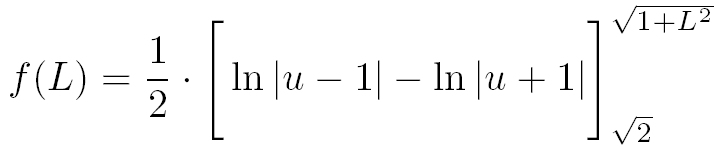
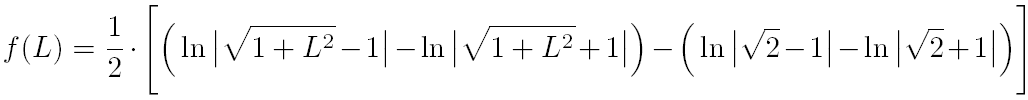
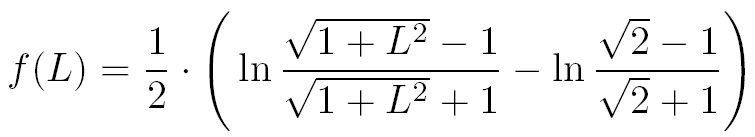
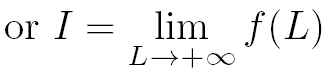
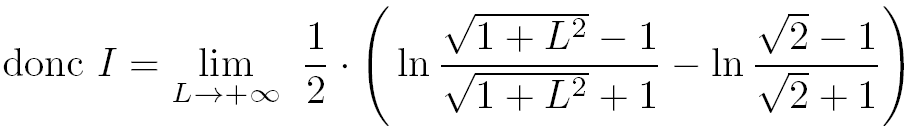
Après le changement de variable et la décomposition en éléments simples, le calcul de l'intégrale I revient à faire un simple calcul de limite.
Etape 3 : le calcul de la limite
En faisant tendre L vers l'infini on en déduit que :
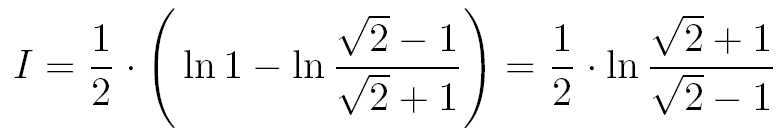
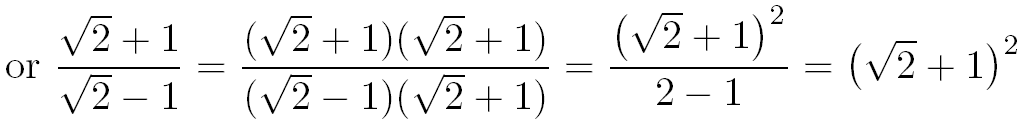
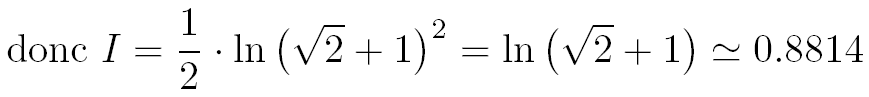
Conclusion
Nous venons de démontrer le résultat final suivant pour l'intégrale I :
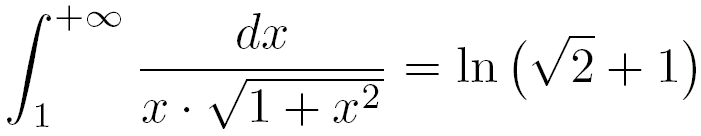
Remarques complémentaires
En notant sinh(x) la fonction sinus hyperbolique d'un nombre réel x, et argsinh(x) sa fonction réciproque voici rapidement (sans les démontrer et en négligeant un peu la rigueur mathématique) quelques relations faisant intervenir notre intégrale I. Pour être complet et exact il faudrait rappeler les conditions d'application de chaque relation ainsi que l'ensemble de définition de chacune des fonctions employées, ce qui n'est pas précisé ici afin d'aller à l'essentiel (et oui, c'est ça la vulgarisation mathématique !).
Rappel des relations de base entre sinh(x) et argsinh(x) :
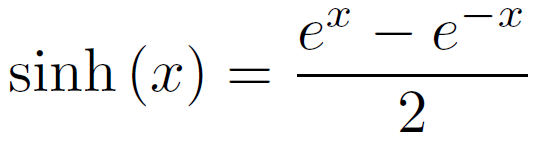

La fonction réciproque de sinh(x) est argsinh(x):
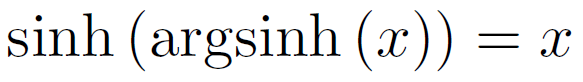
La fonction réciproque de argsinh(x) est sinh(x):
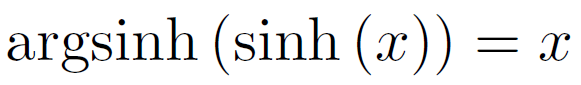
Si on calcule la fonction réciproque de sinh(x) en partant de sa définition donnée ci-dessus avec les exponentielles, on obtient (non démontré ici bien que démontrable) :
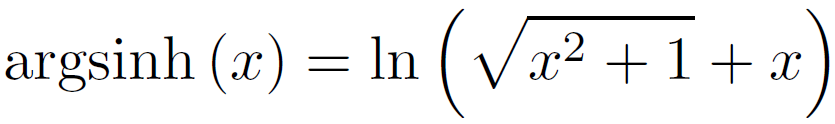
Mais quel rapport existe-t-il entre la fonction argsinh(x) et notre intégrale I ?
Et bien sachant que :
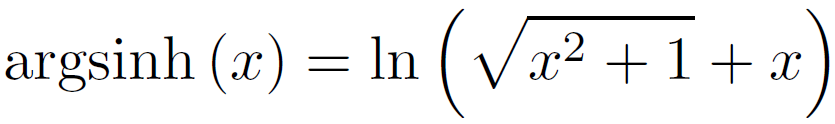
On en déduit que (ça vous rappelle rien ??) :
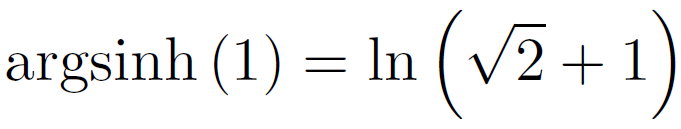
Notre intégrale I vaut donc :
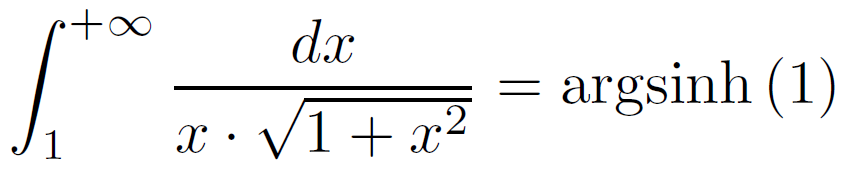
Voici donc une autre écriture en valeur exacte pour I :
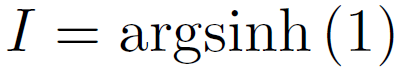
Conclusion : le sinus hyperbolique de I est égal à l'unité, ou si vous péférez : "l'intégrale I est égale à l'unique réel dont le sinus hyperbolique vaut 1". Cet "unique réel" est :
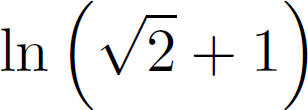
Pour aller plus loin :
EXEMPLE 2 |
Comment calculer la valeur exacte de l'intégrale I suivante ?
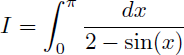
Solution :
La fonction à intégrer est une fraction rationnelle en sin(x) que l'on ne sait pas intégrer : un changement de variable peut alors la convertir en une simple fraction rationnelle en t que l'on saura intégrer.
En appliquant la règle de Bioche on effectue le changement de variable suivant afin de convertir la fonction à intégrer en une fraction rationnelle en t :
Rappel de trigonométrie : pour tout x réel on a sin(2.arctan(x)) = (2.x)/(1+x²)
L'intégrale I devient alors une simple fraction rationnelle en t :
En remarquant que :
Et en connaissant la primitive suivante donnée par la table des primitives :
On obtient :
L'intégale I est égale à la limite de l'intégrale suivante quand α tend vers π :
Grâce au changement de variable on obtient :
La valeur de I est la limite quand α tend vers π :
Et en prenant la limite quand α tend vers π on en déduit la valeur exacte de I :
EXEMPLE 3 |
Comment calculer la valeur exacte de l'intégrale I suivante ?
Solution :
La fonction à intégrer n'est pas une fraction rationnelle en sin(x) et cos(x) en raison du terme x présent au numérateur : nous ne pouvons donc pas appliquer les règles de Bioche pour la convertir en simple fraction rationnelle.
Pour résoudre ce problème et arriver à la valeur numérique exacte de I nous allons effectuer 2 changements de variable successifs.
On effectue un premier changement de variable afin de supprimer le x du numérateur :
L'intégrale I devient :
Ce qui nous donne une nouvelle expression pour I sans le terme x au numérateur :
En appliquant la règle de Bioche on effectue un second changement de variable afin d'obtenir une fraction rationnelle en t :
Et on en déduit la valeur de I :
EXEMPLE 4 |
Comment calculer la valeur exacte de l'intégrale I suivante ?
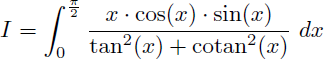
Solution :
La fraction à intégrer n'est pas définie pour x=0 ni pour x=π/2 en raison de tan(x) et cotan(x) au dénominateur. Commençons donc par la ré-écrire.
Sachant que :
Pour 0 < x < π/2 on a :
Et sachant que :
On en déduit que :
Soit :
Cela permet d'écrire l'intégrale I sous une nouvelle forme qui ne pose plus de problème en 0 et en π/2 :
Mais la nouvelle forme obtenue n'est pas une fraction rationnelle en sin(x) en raison du terme x au numérateur : nous ne pouvons donc pas appliquer les règles de Bioche pour la convertir en simple fraction rationnelle.
Pour résoudre ce problème et arriver à la valeur numérique exacte de I nous allons effectuer 3 changements de variable successifs.
On effectue un premier changement de variable :
L'intégrale I devient :
Et en séparant l'intégrale en deux on reconnaît l'intégrale I elle-même dans la seconde intégrale :
Nous obtenons finalement une nouvelle expression de I sans le terme x au numérateur :
Pour obtenir une fraction rationnelle en sin(u) on effectue un second changement de variable :
La fraction rationnelle en sin(u) à intégrer est de la forme suivante :
Décomposons-la en éléments simples :
On en déduit que :
La première intégrale se calcule facilement :
Pour la seconde intégrale, commençons par la ré-écrire :
Pour obtenir une fraction rationnelle en y on effectue un troisième changement de variable dicté par les règles de Bioche :
Ce qui donne :
Soit au final pour l'intégrale I :
EXEMPLE 5 |
Comment calculer la valeur exacte de l'intégrale I suivante ?
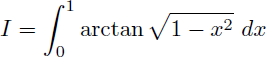
Solution :
La présence de la racine carrée de 1-x² impose que x soit forcément compris entre -1 et 1 :
Cela nous insite (et nous autorise) à effectuer le premier changement de variable suivant :
L'intégrale I devient :
Effectuons une intégration par parties en posant :
Rappel de la dérivée d'arctan(u) :
Rappel de la formule de l'intégration par parties :
On obtient :
Et comme :
L'intégrale I devient :
Il nous faut maintenant calculer l'intégrale J suivante qui est une fraction rationnelle en cos(t) :
Rappel de trigonométrie :
En appliquant les règles de Bioche, effectuons le changement de variable u=tan(t) sur l'intégrale J :
Avec ce changement de variable on obtient :
Or l'intégrale J est la limite en π/2 de l'intégrale suivante :
Et comme tan(0) = 0 et tan(π/2) = +∞, avec le changement de variable précédent J est également la limite en +∞ de l'intégrale suivante :
On en déduit alors la valeur numérique de l'intégrale J :
Et comme on a :
On en déduit la valeur exacte de l'intégrale I :
EXEMPLE 6 |
Comment calculer la valeur exacte de l'intégrale I suivante ?
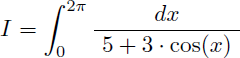
Solution :
Remarquons déjà que comme cos(x) est compris entre -1 et 1, on a 5+3.cos(x) qui est positif entre 0 et 2π, et on en déduit que l'intégrale I est forcément strictement positive :
Comme il s'agit d'intégrer une fraction rationnelle en cos(x), on effectue le désormais classique changement de variable t=tan(x/2) :
Rappel de trigonométrie : pour tout x réel on a cos(2.arctan(x)) = (1-x²)/(1+x²)
L'intégrale I devient :
Or, d'après le tableau des primitives on a :
Mais après le changement de variable, les bornes 0 et 2π deviennent 0 et ... 0 ! Sans réflexion on pourrait donc avoir envie d'écrire :
Ce qui est faux puisque I est strictement positive !
En réalité t n'est pas défini lorsque x traverse la valeur π. La correspondance des intervales entre x et t est la suivante :
En effet, t tend vers l'infini lorsque x tend vers π. Pour résoudre ce problème nous allons découper l'intégrale en deux :
- pour x (avant le changement de variable ) : entre 0 et π puis entre π et 2π
- pour t (après le changement de variable ) : entre 0 et +∞ puis entre -∞ et 0
Nous avons ainsi :
Ce qui permet d'en déduire la vraie valeur de I :
Et comme prévu au début de cet exemple 6 l'intégrale I est bien strictement positive.
Cet exemple 6 a montré que parfois une intégrale définie (c'est-à-dire une intégrale ne posant aucun problème de limite à ses bornes) peut se transformer en intégrale impropre (c'est-à-dire une intégrale nécessitant un calcul de limite à ses bornes) après un changement de variable.
Pour aller plus loin :
Cliquez ici pour obtenir les techniques d'intégration par parties
Cliquez ici pour obtenir les techniques d'intégration par décomposition en éléments simples
Cliquez ici pour obtenir les autres techniques d'intégration