Initiation à la mécanique en Sciences de l'Ingénieur

Cette page explique avec des mots simples et des notions de base les principes fondamentaux de la mécanique. La mécanique est le domaine de la physique qui s'intéresse aux mouvements et à leurs causes. Nous limiterons notre étude à la mécanique du point et à la mécanique du solide, en divisant la discipline "mécanique" en deux sous-disciplines :

• la cinématique : étude du mouvement des corps, indépendamment des forces qui les produisent
• la dynamique : étude du mouvement des corps, en relation avec les forces qui les produisent

La statique sera vue ici comme un cas particulier de la dynamique, et la compréhension de l'ensemble des concepts passera par 4 niveaux :

1 - maîtrise des unités de mesure est des relations entre elles

2 - connaissance des composants mécaniques élémentaires

3 - compréhension des actions mécaniques et de leurs effets

4 - définition des outils permettant de modéliser les actions mécaniques

Sommaire de cette page

Grandeurs physiques et unités de mesure Position, vitesse et accélération Grandeurs scalaires et grandeurs vectorielles Notion d'action mécanique Poids, masse et champ de pesanteur Coefficient de frottement Cinématique Les mécanismes de transformation du mouvement Dynamique

 

Retour au sommaire

Commençons par rappeller le nom et les relations entre les unités de mesure élémentaires, et les unités de mesure propre à la mécanique. La maîtrise des unités de mesure dans le système international, ainsi que les relations entre ces unités est fondamentale pour la compréhension des différents modèles utilisés en mécanique.

Les 6 unités élémentaires
Nom de l'unité de mesure	Symbole de l'unité de mesure	Nom de la grandeur physique mesurée	Symbole de la grandeur physique
seconde kilogramme	s kg	temps masse	t m
mètre mètre carré	m m2	longueur surface	l S
watt joule	W J	puissance énergie	P W

Remarque : en mécanique l'énergie (en Joule) est parfois appelée "travail", et la force (en Newton) est parfois appelée "effort".

Les 8 unités de mécanique
Nom de l'unité de mesure	Symbole de l'unité de mesure	Nom de la grandeur physique mesurée	Symbole de la grandeur physique
newton pascal	N Pa	force pression	F p
mètre par seconde radian par seconde	m.s-1 rad.s-1	vitesse linéaire vitesse angulaire	v ω
newton mètre mètre par seconde carrée	N.m m.s-2	couple (ou moment d'une force) accélération	c a
kilogramme mètre par seconde kilogramme mètre carré	kg.m.s-1 kg.m2	quantité de mouvement moment d'inertie	q J

Remarque : les unités de mesure mécaniques obsolètes ou hors système international sont à proscrire de nos jours. C'est le cas par exemple du Bar pour la pression (la pression se mesure en Pascal dans le système international, on ne parle donc plus de Bar depuis longtemps), ou du tour par seconde pour la vitesse de rotation (l'unité internationale du scientifique est le radian par seconde). De même, le "travail" n'est pas une grandeur physique : il faut parler d'énergie mesurée en Joule ou en Newton mètre. Un dernier exemple : la puissance mécanique d'un moteur ne se mesure plus en chevaux depuis plusieurs décennies (en fait depuis que la diligence a disparu ...) : elle se mesure exclusivement en watt aujourd'hui !

Avant d'énoncer les relations fondamentales à connaître, rappelons la définition de 4 unités de mesure.

Définition du newton : Force qui communique, à un corps ayant une masse de 1 kilogramme, une accélération de 1 mètre par seconde carrée. Définition du pascal : Pression uniforme qui, agissant sur une surface plane de 1 mètre carré, exerce perpendiculairement à cette surface une force totale de 1 newton. Définition du joule : Energie produite par une force de 1 newton dont le point d'application se déplace de 1 mètre dans la direction de la force. Définition du watt : Puissance d'un système énergétique dans lequel est transférée uniformément une énergie de 1 joule pendant 1 seconde.

Relation produit entre les unités de mesure

Le tableau suivant décrit les 8 relations fondamentales concernant les grandeurs physiques utilisées en mécanique. A partir de chacune des ces relations entre grandeurs physiques (relations appelées familièrement "des formules") nous dégagerons systèmatiquement une relation produit entre les unités de mesure.

Une relation produit est de la forme A = B x C, où A B et C sont 3 unités de mesure distinctes, mais liées. La relation produit A = B x C peut bien sûr s'écrire de 3 manières différentes mais équivalentes : A = B x C <=> B = A / C <=> C = A / B (1 relation produit et 2 relations quotient). De ces 3 écritures strictement équivalentes nous ne garderons que la relation produit A = B x C (à convertir ultérieurement en relation quotient en cas de besoin).

Remarque : en mécanique l'énergie (en Joule) est parfois appelé "travail", la force (en Newton) est parfois appelé "effort", la pression (en Pascal) est parfois appelée "contrainte", et le couple (en Newton Mètre) est parfois appelé "moment".

Les 10 relations fondamentales de mécanique
N°	Désignation	Relation entre les grandeurs	Relation entre les grandeurs physiques en toutes lettres	Relation produit entre les unités
1	Force d'un système statique	F=p.S	force = pression x surface	1 N = 1 Pa x 1 m2
2	Force d'un système dynamique	F=m.a	force = masse x accélération	1 N = 1 kg x 1 m.s-2
3	Puissance d'un système mécanique de rotation	P=c.ω	puissance = couple x vitesse angulaire	1 W = 1 N.m x 1 rad.s-1
4	Puissance d'un système mécanique de translation	P=F.v	puissance = force x vitesse linéaire	1 W = 1 N x 1 m.s-1
5	Energie développée par un système de puissance P pendant un temps t	W=P.t	énergie = puissance x temps	1 J = 1 W x 1 s
6	Energie développée par une force F produisant un déplacement d	W=F.d	énergie = force x déplacement	1 J = 1 N x 1 m
7	Quantité de mouvement d'une masse m se déplaçant à la vitesse v	q=m.v	quantité de mouvement = masse x vitesse linéaire	1 kg.m.s-1 = 1 N.s
8	Energie potentielle de pesanteur d'une masse m à une altitude z	W=m.g.z	énergie = masse x accélération x altitude	1 J = 1 kg x 1 m.s-2 x 1 m
9	Energie dans un système mécanique de rotation	W=(J.ω2)/2	énergie = ½ x moment d'inertie x vitesse angulaire ²	1 J = 1 kg x 1 m2.s-2
10	Energie dans un système mécanique de translation	W=(m.v2)/2	énergie = ½ x masse x vitesse linéaire²	1 J = 1 kg x 1 m2.s-2

Sans oubier que lorsque les grandeurs physiques sont des fonctions du temps :

• la vitesse v(t) est la dérivée du déplacement d(t) par rapport au temps
• l'accélaration a(t) est la dérivée de la vitesse v(t) par rapport au temps
• la puissance P(t) est la dérivée de l'énergie W(t) par rapport au temps

 

Remarques et commentaires :

• dans les relations 2, 7 et 10 la masse m est en kilogramme (et non en gramme)
• la relation 1 nous montre que 1 pascal est égal à 1 newton divisé par 1 mètre carré (1 Pa = 1 N / 1 m² = 1 N x 1 m^-2) : 1 Pa = 1 N.m^-2
• la relation 5 n'est pas propre à un système mécanique et reste valable quelque soit le type d'énergie (électrique, mécanique, ou autre)
• la relation 5 nous rappelle que la réunion d'un watt avec 1 seconde (1 watt pendant un temps d'une seconde) développe une énergie d'un joule, ce qui signifie qu'un joule est strictement équivalent à un watt seconde : 1 J = 1 W.s
• les relations 2 et 10 nous montrent que 1 J = 1 N.m = 1 N x 1 m. En effet la relation 2 nous dit que 1 N = 1 kg x 1 m.s^-2, et en multipliant par 1 mètre on obtient 1 N.m = 1 kg x 1 m².s^-2. Or la relation 6 nous dit que 1 kg x 1 m².s^-2 correspond à 1 joule.
• la relation 6 nous rappelle directement que 1 J = 1 N.m
• les relations 3 et 4 nous donnent deux définitions de la puissance mécanique. La différence entre les deux est que dans la relation 3 le mètre est "accroché" au newton (dans le couple) alors que dans la relation 4 le mètre est "accroché" à la vitesse. Dans les deux cas on en déduit que 1 W = 1 N.m.s^-1
• en multipliant les deux membres de la relation produit entre les unités n°3 par une seconde, et sachant que le radian n'est pas une unité de mesure, on retrouve la relation 1 W.s = 1 N.m
• de même, en multipliant les deux membres de la relation produit entre les unités n°4 par une seconde on retrouve à nouveau la relation 1 W.s = 1 N.m
• la relation 7 nous donne un exemple d'unité composée (le "kilogramme mètre par seconde" : 1 kg.m.s^-1 = 1 kg x 1 m.s^-1) qui ne possède pas de nom ou de "raccourcis" simple (contrairement par exemple au "kilogramme mètre carré par seconde carrée" qui s'appelle un Joule). Cette relation 7 nous dit surtout qu'un solide de masse m élancé à la vitesse linéaire v est chargé d'une quantité de mouvement égale au produit de la masse par la vitesse
• contrairement à la force qui s'annule à vitesse constante (voir la relation 2 donnant le principe fondamental de la dynamique), la quantité de mouvement existe à partir du moment ou la vitesse du solide est non nulle (même à accélération nulle)
• mais sachant que 1 N = 1 kg x 1 m.s^-2 (voir la relation 2) on peut remarquer que le "kilogramme mètre par seconde" n'est autre qu'un newton multiplié par une seconde. On en déduit que la quantité de mouvement se mesure en newton seconde : 1 kg.m.s^-1 = 1 N.s
• en comparant les relations 2 et 7 et leurs unités on peut donc remarquer d'un kilogramme mètre par seconde est équivalent à un newton seconde : 1 kg.m.s^-1 = 1 kg.m.s^-2 x 1 s = 1 N x 1 s = 1 N.s = 1 "newton seconde"
• pour la relation 2, si l'accélération considérée est l'accélération de la pesanteur g, alors la force obtenue correspond au poids : p=m.g
• la relation 5 nous rappelle que la puissance est la dérivée de l'énergie par rapport au temps (multiplication par t = dérivée par rapport à t, et division par t = intégration par rapport à t)
• sachant que l'accélération est la dérivée de la vitesse, les relations 2 et 7 nous disent que la force est la dérivée de la quantité de mouvement : en dérivant la relation 7 par rapport au temps on obtient la relation 2 (m étant constante)

 

Récapitulatif des nouvelles relations suite aux remarques précédentes

Concernant les unités de mesure il faut retenir que :

1 N.m = 1 J = 1 W.s	énergie
1 N.m-2 = 1 Pa	pression
1 N.kg-1 = 1 m.s-2	accélération
1 N.s = 1 kg.m.s-1	quantité de mouvement

 

Concernant les grandeurs physiques, on retient qu'il y a deux manières d'exprimer la puissance mécanique :

puissance = couple x vitesse angulaire = force x vitesse linéaire

Ce qui nous conduit à deux définitions de l'énergie mécanique (en multipliant la relation précédente par le temps, c'est-à-dire en l'intégrant) :

énergie = couple = force x longueur

Ce qui nous rappelle une fois de plus que le joule est équivalent au newton mètre : 1 J = 1 N.m

 

Et la notion de quantité de mouvement nous a permis de remarquer que 1kg.m.s^-1 = 1 N.s, soit :

masse x vitesse linéaire = force x temps

Ce qui revient au principe fondamental de la dynamique (en divisant la relation précédente par le temps, c'est-à-dire en la dérivant) :

masse x accélération = force

Ce qui nous ramène au point de départ, à savoir la définition du Newton : 1 kg.m.s^-2 = 1 N

Enfin on déduira également que l'accélération est le rapport entre la force et la masse : 1 m.s^-2 = 1 N.kg^-1

Application : l'accélération de la pesanteur g peut aussi bien s'exprimée en mètre par seconde carrée qu'en newton par kilogramme : g = 9.81 m.s^-2 = 9.81 N.kg^-1

La boucle est bouclée et tout ceci est donc parfaitement cohérent.

En complément de ces bases voir la notion de trajectoire, position, vitesse, accélération et équations horaires.

 

Retour au sommaire

Nous nous limitons ici au mouvement d'un point à accélération constante.

Cas du mouvement linéaire : le point se déplace sur une ligne droite et sa position évolue dans le temps.

Mouvement linéaire
Nom de la grandeur physique	Symbole de la grandeur physique	Nom de l'unité de mesure	Symbole de l'unité de mesure
position vitesse linéaire accélération linéaire	x v a	mètre mètre par seconde mètre par seconde carrée	m m.s-1 m.s-2

Comme la position et la vitesse évoluent dans le temps il faut les mesurer à différents instants. Notons :

• t_i l'instant initial
• t_f l'instant final
• x_i la position à l'instant initial
• x_f la position à l'instant final
• v_i la vitesse à l'instant initial
• v_f la vitesse à l'instant final

 

On note Δt le temps écoulé entre t_i et t_f : Δt = t_f - t_i

On note Δx la distance parcourue entre x_i et x_f : Δx = x_f - x_i

On note Δv l'écart entre la vitesse initiale et la vitesse finale : Δv = v_f - v_i

 

La vitesse moyenne du point entre les instants t_f et t_i est v = Δx / Δt

Remarque : si x_f = x_i le point n'a pas bougé et sa vitesse est nulle.

 

L'accélération du point entre les instants t_f et t_i est a = Δv / Δt

Remarque : si v_f = v_i la vitesse est constante et l'accélération est alors nulle.

 

Lien entre la vitesse et l'accélération :

• la relation entre Δv et a est Δv = a.Δt
• et comme Δv = v_f - v_i
• on en déduit que v_f = v_i + a.Δt

Remarque : si l'accélération a n'est pas nulle la vitesse augmente linéairement en fonction du temps.

 

Position à un instant t en fonction de l'accélération :

• la relation entre Δx et a est Δx = v_i.t + (a.t²)/2
• et comme Δx = x_f - x_i
• on en déduit que x_f = x_i + v_i.t + (a.t²)/2

Remarque : si l'accélération a n'est pas nulle la distance augmente en fonction du carré du temps.

 

Si l'accélération a est nulle (vitesse constante) on en déduit que la position du point à l'instant t en fonction de la position initiale et de la vitesse est : x_f = x_i + v_i.t que l'on peut retenir sous la forme x(t) = x_i + v.t

 

Déplacement d'un point en ligne droite à vitesse constante ou nulle :

A l'instant t₀ le point est immobile à la position x₀.

Entre les instants t₁ et t₂ la position évolue de x₀ à x₁ à une vitesse constante v₁.

Après l'instant t₂ le point est à nouveau immobile.

Voici la courbe d'évolution de la position en fonction du temps :

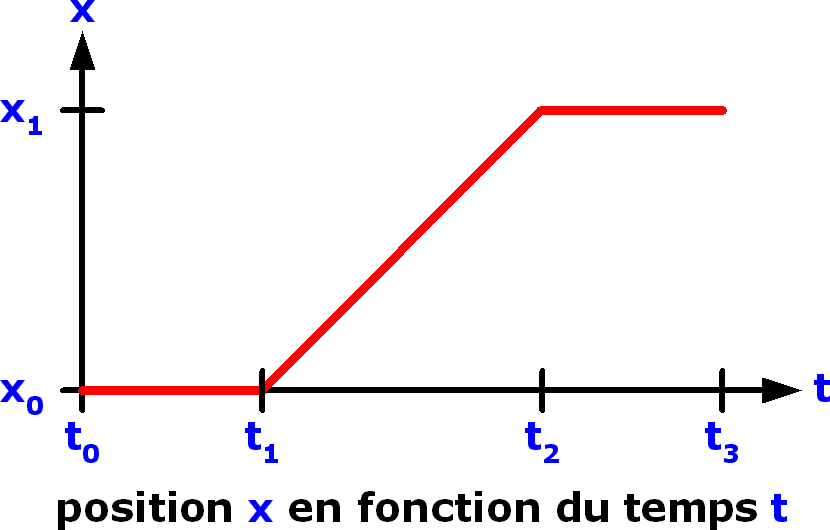
La courbe de la position montre que :

• entre t₀ et t₁ la position est constante et vaut x₀

• entre t₁ et t₂ la position évolue linéairement de x₀ à x₁

• entre t₂ et t₃ la position est constante et vaut x₁

Et voici la courbe d'évolution de la vitesse en fonction du temps :

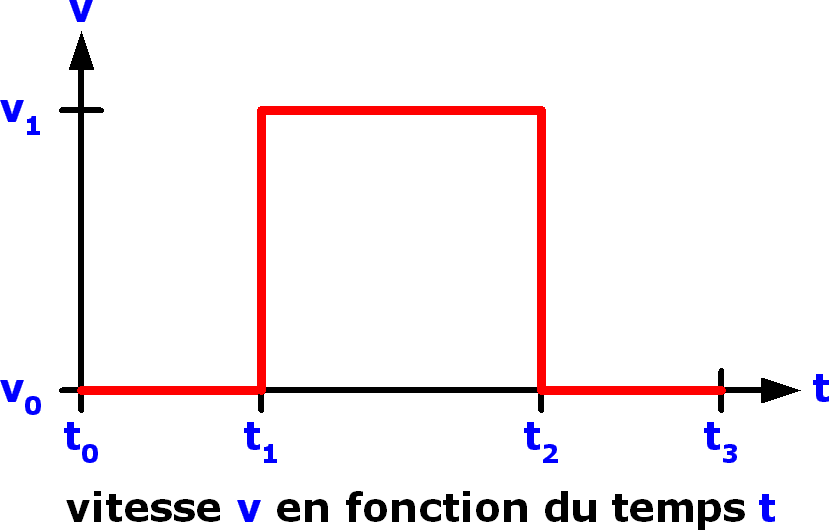
La courbe de la vitesse montre que :

• entre t₀ et t₁ la vitesse est nulle et vaut v₀

• entre t₁ et t₂ la vitesse est positive et vaut v₁

• entre t₂ et t₃ la vitesse est nulle et vaut v₀

De ces deux courbes on en déduit la valeur de la vitesse v₁ : v₁ = Δx / Δt = (x₁ - x₀) / (t₂ - t₁)

 

Déplacement d'un point en ligne droite à accélération constante ou nulle :

A l'instant t₀ le point accélère.

Entre les instants t₁ et t₂ la vitesse est constante et vaut v₁.

Après l'instant t₂ le point ralentit.

Voici la courbe d'évolution de la vitesse en fonction du temps :

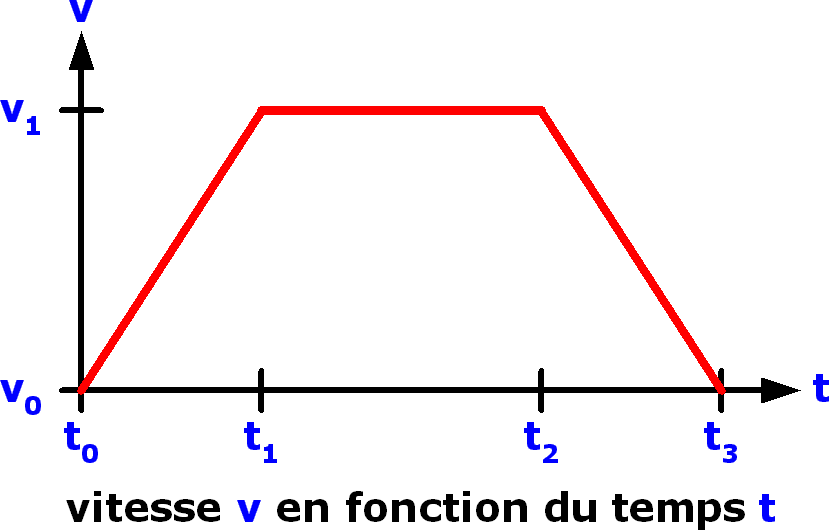
La courbe de la vitesse montre que :

• entre t₀ et t₁ la vitesse est croissante et évolue linéairement de v₀ à v₁

• entre t₁ et t₂ la vitesse est constante et vaut v₁

• entre t₂ et t₃ la vitesse est décroissante et évolue linéairement de v₁ à v₀

 

Et voici la courbe d'évolution de l'accélération en fonction du temps :

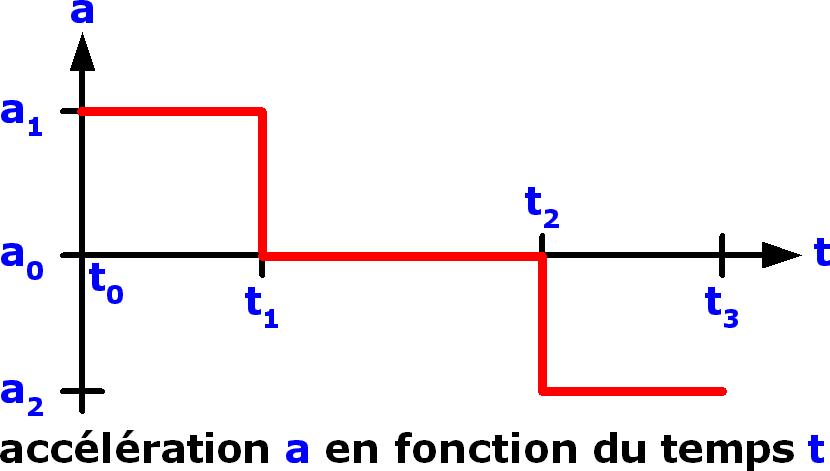
La courbe de l'accélération montre que :

• entre t₀ et t₁ l'accélération est positive et vaut a₁

• entre t₁ et t₂ l'accélération est nulle

• entre t₂ et t₃ l'accélération est négative et vaut a₂

De ces deux courbes on en déduit la valeur de l'accélération a₁ et de la décélération (accélération négative) a₂ :

a₁ = Δv / Δt = (v₁ - v₀) / (t₁ - t₀)

a₂ = Δv / Δt = (v₀ - v₁) / (t₃ - t₂)

 

Déplacement d'un point en ligne droite à accélération constante :

On note :

a l'accélération constante (en m/s²)

v la vitesse à l'instant t (en m/s, et notée aussi v(t))

x la position à l'instant t (en m, et notée aussi x(t))

v₀ la vitesse initiale (en m/s, et correspondant à v(0))

x₀ la position initiale (en m, et coorespondant à x(0))

v et x évoluent dans le temps : ces fonctions ont donc une dérivée non nulle.

a, v₀ et x₀ sont constants dans le temps.

L'accélération est le dérivée de la vitesse : a = dv/dt

La vitesse est la dérivée de la position : v = dx / dt

On en déduit les fonction v(t) et x(t) sachant que l'accélération a est constante :

La vitesse est la primitive de l'accélération : v = a.t + v₀ (1)

La position est la primitive de la vitesse : x = 1/2.a.t² + v₀.t +x₀ (2)

D'après (1) il vient : a = (v-v₀)/t

D'après (2) il vient : x - x₀ = 1/2.a.t² + v₀.t = (v-v₀).t/2 + v₀.t

On en déduit que 2.(x - x₀) = (v-v₀).t + 2.v₀.t

Et donc : 2.a.(x - x₀) = (v-v₀)² + 2.v₀.(v-v₀) = v²-v₀²

 

Soit au final : v² = v₀² + 2.a.(x - x₀)

 

En appelant d le déplacement x - x₀ on en déduit la relation suivante donnant instantanément d connaissant a, v et v₀ :

 

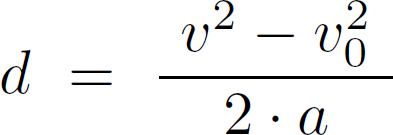
Remarque : le déplacement étant la primitive de la vitesse il peut aussi s'obtenir par un simple calcul d'aire sur la courbe v(t). Exemple :

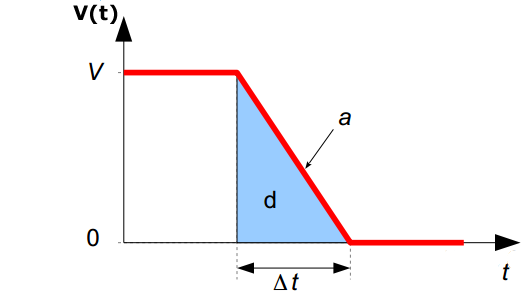
La courbe ci-dessus montre l'évolution de la vitesse d'un train pendant la phase de freinage. Le train passe de la vitesse V à la vitesse 0 en un temps Δt avec une décélération a. La distance d parcourue par le train durant la phase de freinage est simplement l'aire du triangle bleu :

d = (Δt.V)/2

Et comme Δt = V/a on en déduit que la distance d vaut :

d = (V/a . V)/2 = V²/(2.a)

Ce qui correspond à la relation complète ci-dessus avec v₀ = 0.

 

Cas du mouvement circulaire : le point a une trajectoire en forme de cercle et sa position (un angle) évolue dans le temps.

Mouvement circulaire
Nom de la grandeur physique	Symbole de la grandeur physique	Nom de l'unité de mesure	Symbole de l'unité de mesure
position vitesse angulaire accélération angulaire	θ ω γ	radian radian par seconde radian par seconde carrée	rad rad.s-1 rad.s-2

Le principe est le même que précédemment en remplaçant la distance (en mètre) par un angle (en radian).

 

Conversion de la vitesse angulaire en vitesse linéaire :

Un point A appartenant à la périphérie d'un disque de rayon R tournant à la vitesse angulaire ω se déplace avec une vitesse linéaire v :

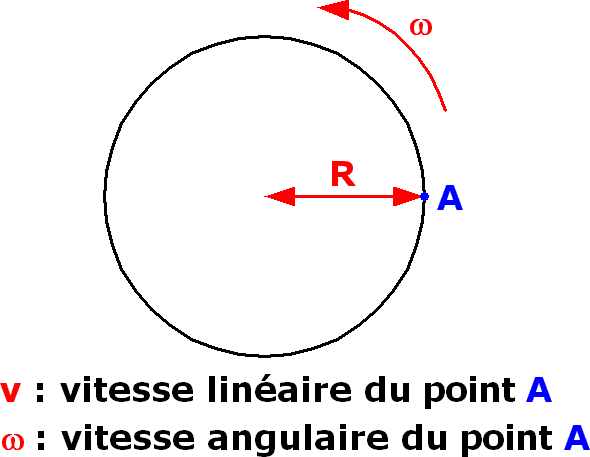
Le lien entre R, ω et v est alors le suivant :

v = ω.R

avec :

• v la vitesse linéaire du point A en mètre par seconde

• ω la vitesse angulaire du point A en radian par seconde

• R la distance entre le point A et l'axe de rotation (rayon du disque) en mètre

Rappel de la définition du radian : un angle d'un radian intercepte sur la circonférence du cercle un arc d'une longueur égale au rayon.

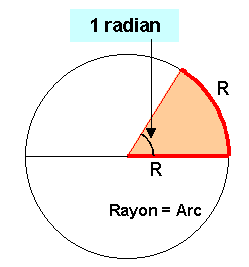
Donc si la position angulaire du point A augmente de 1 radian, le point A parcourt une distance égale à R.

Et comme le point A évolue de ω radian par seconde, il parcourt R fois ω mètre par seconde, d'où v=ω.R

 

Retour au sommaire

On appelle grandeur scalaire une grandeur physique qui peut se résumer à un simple nombre lié à une unité de mesure. Exemple de grandeurs scalaires : le temps, la masse, la longueur, l'énergie, etc.

On appelle grandeur vectorielle une grandeur physique qui est définie par :

• un nombre lié à une unité de mesure
• un sens
• une direction

 

Pourquoi a-t-on besoin d'utiliser des grandeurs vectorielles ?

En mécanique, pour être définies certaines grandeurs ont besoin d'être repérées dans un plan (en 2D) ou dans l'espace (en 3D). C'est la cas par exemple de la position d'un point : pour décrire la position d'un point il faut 2 coordonnées dans un plan, ou 3 composantes dans l'espace. Le modèle utilisé pour rassembler les coordonnées est alors le vecteur. La position est donc une grandeur vectorielle : elle ne peut pas se résumer à une seule valeur. On parle alors de "vecteur position", et sa norme est exprimée en mètre.

Toutes les grandeurs dérivées d'une grandeur vectorielle est également une grandeur vectorielle :

• la vitesse est la dérivée de la position par rapport au temps : la vitesse est donc une grandeur vectorielle
• l'accélération est la dérivée de la vitesse par rapport au temps : l'accélération est donc une grandeur vectorielle

De plus on sait que le poids P d'un corps de masse m est définit par P = m.g avec g l'accélération de la pesanteur. Comme m (la masse) est scalaire et g (l'accélération) est vectorielle, on en déduit que le poids P est une grandeur vectorielle. Et comme de manière générale la force est égale au produit de la masse par l'accélération linéaire (d'après le principe fondamental de la dynamique F=m.a avec m la masse scalaire et a l'accélaration vectirielle), on en déduit que la force est également une grandeur vectorielle, c'est-à-dire définie par une valeur (en Newton), une direction et un sens, le tout étant modélisé par un vecteur.

 

Quelques grandeurs scalaires et vectorielles

Voici la nature (scalaire ou vectorielle) des grandeurs physiques usuelles utiliées en mécanique :

Les grandeurs scalaires et les grandeurs vectorielles
Grandeur physique	Unité de mesure	Nature de la grandeur
le temps	seconde	scalaire
la longueur	mètre	scalaire
la masse	kilogramme	scalaire
la puissance	watt	scalaire
l'énergie	joule	scalaire
le couple	newton mètre	scalaire
la position (ou le déplacement)	mètre	vectorielle
la vitesse	mètre par seconde	vectorielle
l'accélération	mètre par seconde carrée	vectorielle
le poids	newton	vectorielle
la force	newton	vectorielle
le moment d'une force	newton mètre	vectorielle

Ce tableau n'est pas exhaustif mais suffit pour trouver la nature des autres grandeurs.

Exemple 1 : quelle est la nature de la quantité de mouvement q ? Comme q=m.v, la quantité de mouvement est le produit d'une grandeur scalaire (la masse m) et d'une grandeur vectorielle (la vitesse v) : on en déduit que la quantité de mouvement q est une grandeur vectorielle.

Exemple 2 : quelle est la nature du déplacement entre un point A et un point B ? Par définition le déplacement entre un point A et un point B est égal à la différence des positions des points A et B. Comme la position est vectorielle, le déplacement est également vectoriel puisque la différence entre deux vecteurs donne un vecteur, et sera dans ce cas modélisé par le vecteur AB.

Ce tableau fait également apparaître la différence fondamentale entre la masse et le poids. La différence entre ces deux grandeurs physiques n'est pas seulement un raport de 9.81 avec un changement d'unité de mesure, mais est surtout le changement de nature : alors que la masse est simplement scalaire, le poids lui est vectoriel.

Même remarque entre le couple et le moment. La différence entre ces deux grandeurs physiques (qui se mesurent toutes les deux en newton mètre, produit d'une force par une distance), est encore le changement de nature : alors que le couple est simplement scalaire, le moment lui est vectoriel : le couple est en fait la norme du vecteur moment (tout comme la longueur est la norme du vecteur position).

En résumé si une grandeur peut se repérer sur une droite elle est scalaire, si elle doit être repérée dans le plan ou dans l'espace elle est vectorielle :

• si un point se déplace seulement sur une droite, alors sa position, sa vitesse et son accélération seront des grandeurs scalaires (vecteurs à 1 dimension)
• si un point se déplace dans un plan, alors sa position, sa vitesse et son accélération seront des grandeurs vectorielles (vecteurs à 2 dimensions)
• si un point se déplace dans l'espace, alors sa position, sa vitesse et son accélération seront des grandeurs vectorielles (vecteurs à 3 dimensions)

 

Opération entre deux grandeurs

Entre deux grandeurs scalaires les opérations possibles sont les 4 opérations arithmétiques classiques :

• somme
• différence
• produit
• quotient

Les unités de mesure subissent alors les mêmes opérations. Exemple : des mètres divisés par des secondes donnent des mètres par seconde.

Entre une grandeur scalaire et une grandeur vectorielle il existe 2 opérations :

• multiplication d'un vecteur par un scalaire : chaque coordonnées est multipliée par le scalaire
• division d'un vecteur par un scalaire : chaque coordonnées est divisée par le scalaire

Entre deux grandeurs vectorielles il existe 4 opérations possibles :

• la somme de deux vecteurs : on additionne les coordonnées de même nature (abscisses, ordonnées, et cotes)
• la différence de deux vecteurs : on soustrait les coordonnées de même nature (abscisses, ordonnées, et cotes)
• le produit scalaire : le résultat est un scalaire
• le produit vectoriel : le résultat est un vecteur

Rappel des produits scalaire et vectoriel :

Soit V1 un vecteur de coordonnées (x1,y1) et V2 un vecteur de coordonnées (x2,y2) :

$$\overrightarrow{V_1}=\left|\begin{array}{c} x_1\\ y_1\\ \end{array}\right.$$

$$\overrightarrow{V_2}=\left|\begin{array}{c} x_2\\ y_2\\ \end{array}\right.$$

La norme de chaque vecteur est donnée par le théorème de Pythagore :

$$\|\overrightarrow{V_1}\|=\sqrt{x_1^2+y_1^2}$$

$$\|\overrightarrow{V_2}\|=\sqrt{x_2^2+y_2^2}$$

Notons S le résultat du produit scalaire entre les vecteurs V1 et V2 :

$$S=\overrightarrow{V_1}\cdot \overrightarrow{V_2}$$

La valeur numérique de S est donnée par la relation suivante :

$$S=\|\overrightarrow{V_1}\|\cdot \|\overrightarrow{V_2}\|\cdot \cos(\overrightarrow{V_1}\overrightarrow{V_2})=x_1\cdot x_2+y_1\cdot y_2$$

Remarque : si deux vecteurs sont orthogonaux alors leur produit scalaire est nul.

 

Notons V le résultat du produit vectoriel entre les vecteurs V1 et V2 :

$$\overrightarrow{V}=\overrightarrow{V_1}\land \overrightarrow{V_2}$$

La norme du vecteur V est donnée par la relation suivante :

$$\|\overrightarrow{V}\|=\|\overrightarrow{V_1}\|\cdot \|\overrightarrow{V_2}\|\cdot \sin(\overrightarrow{V_1}\overrightarrow{V_2})=x_1\cdot y_2-y_1\cdot x_2$$

Remarque : si deux vecteurs sont colinéaires alors la norme de leur produit vectoriel est nulle.

Les coordonnées du résultat du produit vectoriel de deux vecteurs dans l'espace sont données par les relations suivantes :

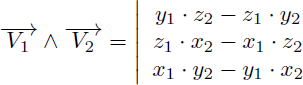
En mécanique, la force est un vecteur et :

• le travail d'une force est un produit scalaire (donc une grandeur scalaire)
• le moment d'une force est un produit vectoriel (donc une grandeur vectorielle)

 

Retour au sommaire

L'action mécanique est un concept utilisé en mécanique pour décrire tous les phénomènes provoquant un mouvement ou une déformation. Ce concept regroupe les notions de force et de moment utilisées en mécanique.

Une action mécanique est un phénomène physique capable de :

• créer un déplacement
• maintenir un corps en équilibre
• déformer un corps

Les actions mécaniques sont de deux sortes :

• les actions mécaniques à distance (champ de pesanteur, champ électromagnétique,…)
• les actions mécaniques de contact, exercées par un solide sur un autre solide par l’intermédiaire de leur surface de contact

Une force à distance particulière : la pesanteur

La pesanteur ou attraction terrestre agit sur tous les solides sous la forme d’une force résultante, dont les caractéristiques sont les suivantes :

• Point d’application : G, centre de gravité du solide
• Direction : verticale
• Sens : vers le bas
• Intensité : P = m x g (P en Newton)

Avec :

• m : masse du solide (en kg)
• g : accélération de la pesanteur g = 9,81 N/kg = 9,81 m/s²

Cette force notée  $\overrightarrow{P}$ s’appelle le poids (en Newton) et est une grandeur vectorielle.

Le moment d'une force par rapport à un point donné est une grandeur physique vectorielle traduisant l'aptitude d'une force à faire tourner un système mécanique autour de ce point, appelé souvent pivot. Il s'exprime en N.m (newton-mètre).

Deux type d'actions mécaniques peuvent s'exercer sur un solide : les forces et les moments.

La somme vectorielle de toutes les forces s'appliquant sur un solide est appelée la force résultante (ou parfois tout simplement "la résultante"). Si la force résultante est égale au vecteur nul alors le solide est immobile (exemple : un objet posé sur une table est soumis à 2 forces opposées dont la somme est nulle).

La somme vectorielle des moments en un point créés par toutes les forces s'appliquant sur un solide est appelée le moment résultant. Si le moment résultant au point considéré est égal au vecteur nul alors la liaison pivot en ce point n'est pas en mouvement. Exemple : une balance à contre-poids est en équilibre si le moment résultant au point d'articulation est nul.

Pour connaître l'ensemble des actions mécaniques appliquées à un solide il faut donc préciser à la fois le vecteur de la force résultante et le vecteur du moment résultant.

Un torseur est un outils permettant de modéliser complètement une action mécanique : le torseur réunit en un seul élément les coordonées des vecteurs force résultante et moment résultant. Comme première utilisation le torseur permet tout simplement de représenter ces deux informations ensemble.

En mécanique, modéliser consiste à représenter un problème réel sous une forme mathématique :

• une grandeur scalaire se modélise par un scalaire (associé à une unité de mesure)
• une grandeur vectorielle se modélise par un vecteur (ensemble de scalaires)
• en mécanique pour réunir ensemble plusieurs vecteurs on utilise un torseur

Exemple : vecteur de la force résultante + vecteur du moment résultant en un point A = torseur de l'action mécanique au point A

Voici par exemple le torseur exprimant entièrement les actions mécaniques s'exerçant sur un solide soumis uniquement à son poids : il y a alors une seule action mécanique, une force verticale (d'axe y) dirigée vers le bas (négative) et d'intensité m.g. Le moment résultant (seconde colonne du torseur) est nul dans ce cas :

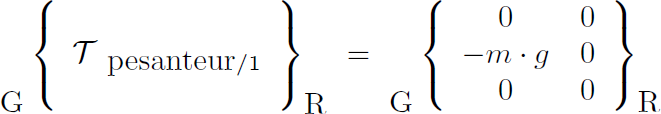
Torseur des actions mécaniques de la pesanteur sur le solide 1 au point G dans le repère R

 

Réduction d'un torseur :

Réduire un torseur consiste à écrire les composantes du torseur en un point B connaisant le torseur au point A. Dans un torseur, la résultante est invariante, seul le moment varie en fonction du centre de réduction (point d'application du torseur). Pour exprimer un torseur au point B connaissant le torseur au point A on utilise la relation de transport de moment suivante :

$$\overrightarrow{M_B}=\overrightarrow{M_A}+\overrightarrow{BA} \land \overrightarrow{R}$$

 

Torseur des actions mécaniques transmissibles :

Un torseur des actions mécaniques transmissibles permet de modéliser une liaison cinématique en indiquant par des 0 les mouvements autorisés. Exemples :

Voici le torseur des actions mécaniques transmissibles d'une liaison glissière en Y :

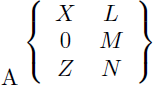
Et voici par exemple le torseur des actions mécaniques transmissibles d'une liaison rotule :

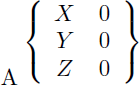
Connaissant les tableaux des mobilités des 11 liaiosns cinématiques, chacune en déduira les 11 torseurs d'actions mécaniques transmissibles correspondant.

 

Retour au sommaire

Le rapport du poids P et de la masse m est égale à l'intensité de la pesanteur : P = m.g

Sur terre g = 9.81 N/kg

Sur la lune g = 1.6 N/kg

Sur Mars g = 3.9 N/kg

Sur Jupiter g = 26 N/kg

Exemple : un objet de masse 1kg posé sur le sol exerce une force de 9.81 N sur terre, 1.6 N sur la lune, 3.9 N sur la planète Mars, et 26 N sur Jupiter.

Il est pratique de considérer le poids comme une force unique dont le point d'application est le centre de gravité de l'objet noté G (qui coïncide avec le centre d'inertie). Le vecteur force  $\overrightarrow{P}$ modélisant la force dûe au poids est vertical et dirigé vers le bas. Afin de faire apparaître la nature vectorielle du poinds on écrit aussi :

$$\overrightarrow{P}=m.\overrightarrow{g}$$

où  $\overrightarrow{g}$ est le vecteur champ de pesanteur : il est vertical et dirigé vers le bas.

$$\|\ \overrightarrow{g}\ \|=9.81 N/kg$$

En réalité sur terre g n'a pas une valeur constante en tout point de la planète. La valeur de g varie légèrement en fonction de la nature du sol, de la latitude, de l'altitude, de la force centrifuge dûe à la rotation de la terre, etc.

g diminue avec l'altitude car on s'éloigne du centre de la terre et varie légèrement avec la latitude du lieu :

• à l'équateur g ≈ 9.78 N/kg
• aux pôles g ≈ 9.83 N/kg

Voici la relation donnant les variations de g en fonction de l'altitude h :

$$g=g_0.\frac{R^2}{\ (R+h)^2\ }$$

avec :

• g₀ = 9.81 N/kg
• R = le rayon de la Terre ≈ 6378 km
• h = l'altitude

Il faut savoir que la valeur de 9.81 N/kg de g₀ n'est qu'une valeur arrondie : pour information la valeur exacte de g₀ est 9.80665 N/kg.

La valeur arrondie de 9.81 N/kg pour g est valable à l'altitude 0 (h=0) et à la latitude de 45° (sur le 45^ème parallèle). Mais dans la pratique on s'accorde à prendre g constant de valeur 9.81 N/kg (sans variation ni plus de précision) pour tous les exercices de mécanique et quelque soit le lieu d'application sur la planète Terre.

 

Retour au sommaire

Force normale et force tangentielle

Lorsqu'un objet est posé sur un plan incliné, le poids (force verticale) se décompose en 2 forces :

• une composante normale notée Pn et perpendiculaire au plan incliné
• une composante tangentielle notée Pt et parallèle au plan incliné

 

Exemple 1 : le skieur sur une pente

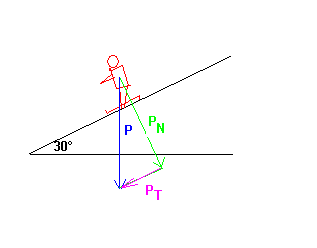
P = Pn + Pt

La composante normale Pn assure le contact entre le skieur et le sol, mais ne participe pas au mouvement.

La composante tangentielle Pt a tendance à vouloir mettre en mouvement le skieur dans le sens de la pente.

Question : la force Pt est-elle suffisante pour que le skieur glisse sur le plan incliné ?

Réponse : tout dépend du rapport Pt/Pn. Si Pt/Pn dépasse une limite µ (mu) alors il y a mouvement. Cette limite µ est appelé le coefficient de frottement et dépend seulement des deux matériaux en contact.

Si Pt/Pn > µ alors il y a mouvement avec frottement

Si Pt/Pn = µ alors il y a adhérence limite (pas de mouvement)

Si Pt/Pn < µ alors il y a adhérence (pas de mouvement)

 

Exemple 2 : un objet immobile sur un plan incliné

Dans le cas où l'objet reste immobile sur le plan incliné, la composante normale comme la composante tangentielle du poids donne lieu à une action mutuelle (force opposée). Exemple d'un objet de masse m immobile sur un plan incliné d'un angle θ (thêta) par rapport à l’horizontale :

La composante normale du poids, ici m.g.cos(θ), crée une force opposée N (force de renvoi du plan incliné sur l'objet)

La composante tangentielle du poids, ici m.g.sin(θ), crée une force opposée f appelé force de frottement et empêchant l'objet de glisser

Tant que la somme vectorielle de ces 4 forces est nulle l'objet reste immobile : c'est la condition d'équilibre. Ainsi, selon le module et l’orientation des autres forces appliquées sur l'objet, la force de frottement statique f va s’ajuster entre les valeurs suivantes pour satisfaire la condition d'équilibre :

0 ≤ f ≤ µ.N

Question : à partir de quelle valeur de l'angle θ l'objet glisse-t-il sur le plan incliné si le coefficient de frottement entre l'objet et le plan incliné est µ ?

Réponse : tant que (m.g.sin(θ)) / (m.g.cos(θ)) est inférieur ou égal à µ l'objet est immobile. L'objet commencera à être en mouvement lorsque (m.g.sin(θ)) / (m.g.cos(θ)) deviendra supérieur à µ

Remarque : (m.g.sin(θ)) / (m.g.cos(θ)) = sin(θ) / cos(θ) = tan(θ)

La condition de mise en mouvement s'écrit donc tan(θ) > µ, soit θ > arctan(µ)

Et la condition d'équilibre peut se résumer à θ ≤ arctan(µ)

On peut remarquer que la condition d'équilibre d'un objet de masse m posé sur un plan incliné dépend seulement de la comparaison entre l'angle d'inclinaison θ du plan incliné et l'arctangente du coefficient de frottement statique µ entre l'objet et le plan incliné, et ne dépend pas de la masse m de l'objet :

Si θ > arctan(µ) alors il y a mouvement avec frottement (l'objet glisse)

Si θ = arctan(µ) alors il y a adhérence limite (l'objet reste immobile)

Si θ < arctan(µ) alors il y a adhérence (l'objet reste immobile)

 

 

Actions mutuelles normale et tangentielle du poids pour un objet immobile sur un plan incliné :

 

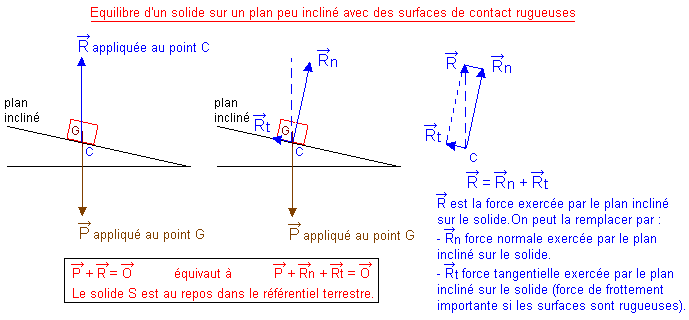
L'angle entre le plan incliné et l'horizontale est toujours égal à l'angle entre le vecteur poids et sa composante normale :

 

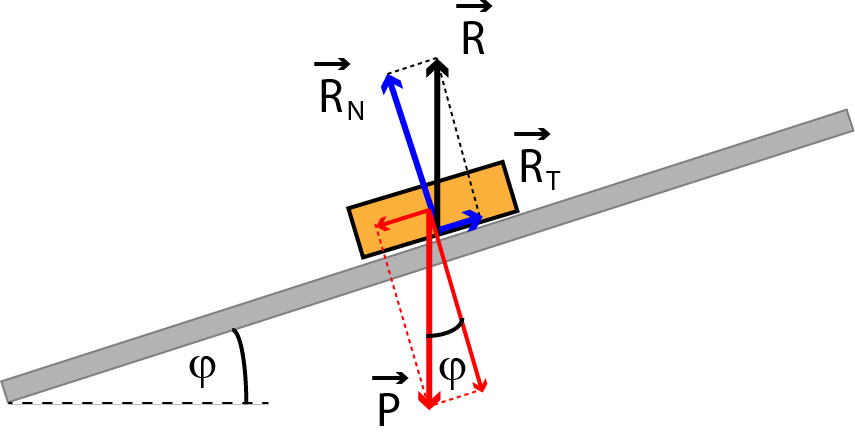
Quelques exemples de valeurs du coefficient de frottement statique µ

Le coefficient de frottement statique µ, qui permet de calculer la limte à partir de laquelle un objet commence à glisser, dépend de la nature des surfaces en contact et ne dépend pas de la masse de l'objet étudié. Le tableau suivant donne quelques exemples de valeurs pour µ.

 

Exemple de coefficient de frottement statique
Nature des surfaces en contact	Valeur de µ (sans unité)
bois sur bois	0.65
glace sur glace	0.1
caoutchouc sur ciment sec	1.0
téflon sur téflon	0.04
acier sur acier	0.18
acier sur fonte	0.19
acier sur bronze	0.11
téflon sur acier	0.04
métaux sur bois	0.5 à 0.6
pneus sur route sèche	0.6 à 0.7
pneus sur route mouillée	0.35 à 0.6
pneus sur route verglassée	0.1

 

 

 

Retour au sommaire

La cinématique est la partie de la mécanique qui étudie le mouvement des corps, indépendamment des forces qui les produisent. Les grandeurs étudiées sont le mouvement, le déplacement, la trajectoire, la vitesse et l'accélération.

La cinématique est la théorie qui, à l’intérieur de la mécanique, a pour objet la description des mouvements des systèmes matériels.

Deux notions sont absolument indispensables à l’élaboration de la cinématique sous sa forme classique : celle de solide invariable et celle de temps. Muni d’un repère à 3 dimensions dans lequel il peut mesurer des longueurs et situer des points géométriques et des solides, muni d’un dispositif chronométrique à l’aide duquel il peut mesurer des durées de manière continue et affecter une date à tout événement instantané, le mécanicien se livre alors à la description des mouvements des systèmes physiques en commençant par le plus simple de ces systèmes, celui qui est constitué d’un seul solide.

Comme en cinématique on étudie le déplacement en fonction du temps, certaines grandeurs physiques seront des fonctions du temps.

Par exemple la vitesse v sera notée v(t) ce qui rappelle que sa valeur instantanée dépend du temps.

La dérivée de v(t) par rapport au temps se note d v(t)/dt ou plus rapidement "v(t) point".

 

La cinématique du point

Un point dans l'espace peut se déplacer dans les 3 directions : en x, en y et en z. Sa position est donc définie avec 3 composantes et il possède 3 degrés de liberté.

Dans le plan, le point possède 2 degrés de liberté et sa position est modélisée par un vecteur à 2 composantes.

Soit M un point de coordonnées (x,y) dans le plan. La position du point est modélisée par le vecteur position OM.

Le vecteur vitesse est la dérivée du vecteur position.

Le vecteur accélération est la dérivée du vecteur vitesse.

On appelle trajectoire de M dans le repère R, l’ensemble des points fixes de R avec lesquels le point M vient en coïncidence dans la succession des événements, ou encore l’ensemble des positions de M dans R.

 

La cinématique du solide

Étudier le mouvement d’un solide, c’est être en mesure d’indiquer la trajectoire, la vitesse et l’accélération de tous les points qui lui sont liés. Le premier de ces trois objectifs n’admet pas de réponse générale : sauf cas particuliers, les trajectoires des différents points liés à un solide n’ont aucun rapport simple ; ainsi, dans le mouvement «en ligne droite» d’une bicyclette, un point lié à un moyeu de roue admet une trajectoire rectiligne par rapport au sol (il est immobile par rapport au cadre), tandis qu’un point de la bande de roulement d’un pneumatique (supposé rigide) admet une trajectoire cycloïdale par rapport au sol (et circulaire par rapport au cadre).

Par contre, dès que sont connues la vitesse et l’accélération d’un point lié au solide, et que la manière dont varie en fonction du temps l’orientation du solide dans le repère est précisée, les vitesses et les accélérations de tous les points liés au solide peuvent être évaluées.

En plus des 3 mouvements de translations, un solide dans l'espace peut aussi effectuer 3 mouvements de rotation autour des axes x, y ou z. Le solide dans l'espace peut donc avoir jusqu'à 6 degrés de liberté : 3 translations et 3 rotations.

Cliquez sur l'image pour télécharger la vidéo de 5 Mo montrant
les 6 déplacements élémentaires d'un solide dans l'espace

Lorsque 2 solides sont liés et en mouvement il existe 11 liaisons cinématiques pour lesquelles la surface de contact est inchangée au cours du mouvement :

Les 11 liaisons cinématiques
Nom de la liaison	Nombre de degrés de liberté	Nombre de degrés de liaison	Nombre de rotations autorisées	Nombre de translations autorisées	Nombre de rotations interdites	Nombre de translations interdites
encastrement	0	6	0	0	3	3
glissière	1	5	0	1	3	2
pivot	1	5	1	0	2	3
pivot glissant	2	4	1	1	2	2
appui plan	3	3	1	2	2	1
rotule	3	3	3	0	0	3
sphère / plan	5	1	3	2	0	1
cylindre / plan	4	2	2	2	1	1
sphère / cylindre	4	2	3	1	0	2
rotule à doigt	2	4	2	0	1	3
hélicoïdale	1	5	1 et 1 liées		2	2

Dans le tableau ci-dessus les deux valeurs en rouge suffisent pour caractériser complètement une liaison. Les 4 valeurs bleues se déduisent des 2 valeurs rouges. On peut remarquer qu'aucune liaison possède 6 degrés de liberté, et aucune liaison autorise les 3 translations.

Remarques :

sphère / plan - 1 translation = sphère / cylindre

sphère / plan - 2 translations = rotule

rotule - 1 rotation = rotule à doit

rotule - 2 rotations = pivot

Le tableau suivant illustre chacune des 11 liaisons cinématiques dans un mécanisme animé et rappelle la mobilité des 6 déplacements élémentaires :

Exemples de mécanismes illustrant chacune des 11 liaisons
Liaison cinématique	Exemple de mécanisme	Tableau des mobilités
encastrement		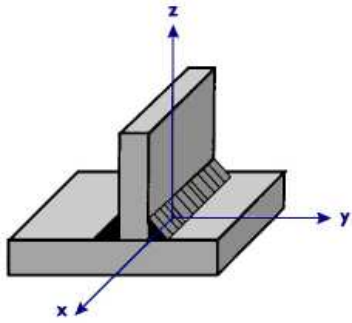Tx = 0 Rx = 0 Ty = 0 Ry = 0 Tz = 0 Rz = 0
glissière		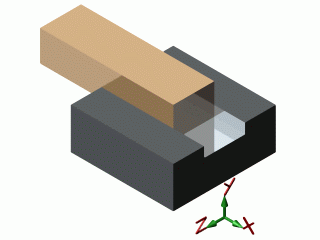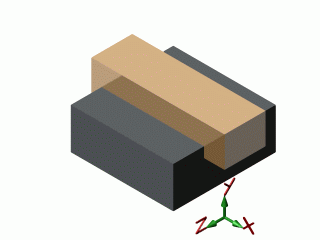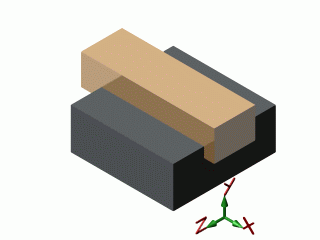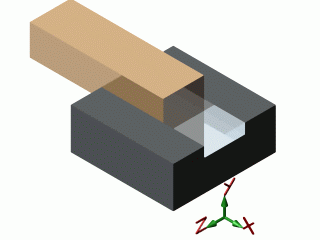Tx = 1 Rx = 0 Ty = 0 Ry = 0 Tz = 0 Rz = 0
pivot		Tx = 0 Rx = 1 Ty = 0 Ry = 0 Tz = 0 Rz = 0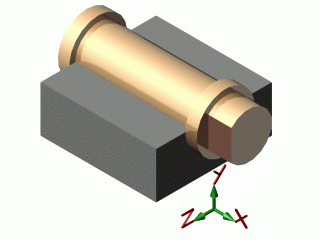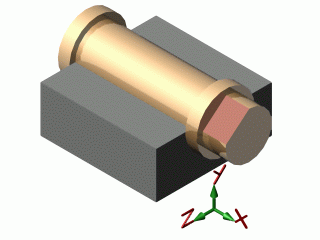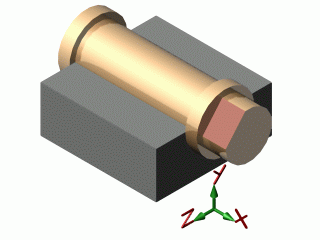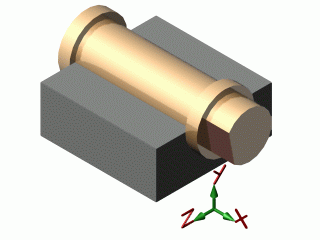
pivot glissant		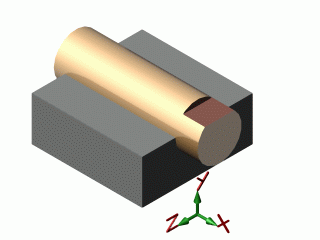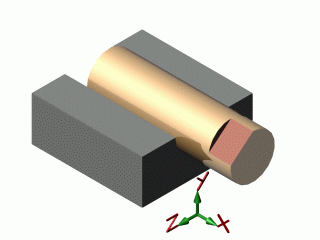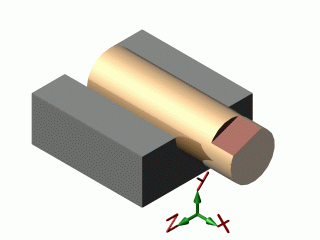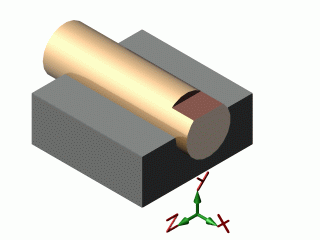Tx = 1 Rx = 1 Ty = 0 Ry = 0 Tz = 0 Rz = 0
appui plan		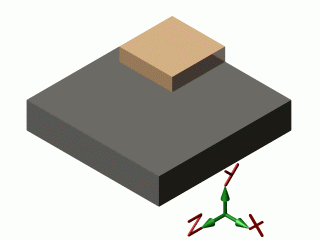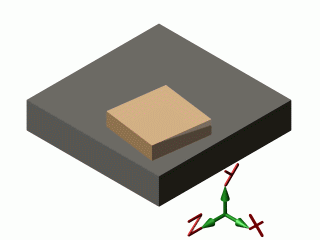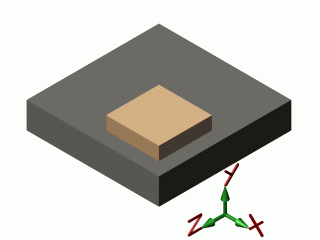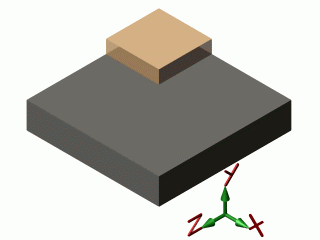Tx = 1 Rx = 0 Ty = 0 Ry = 1 Tz = 1 Rz = 0
rotule		Tx = 0 Rx = 1 Ty = 0 Ry = 1 Tz = 0 Rz = 1
sphère / plan		Tx = 1 Rx = 1 Ty = 0 Ry = 1 Tz = 1 Rz = 1
cylindre / plan		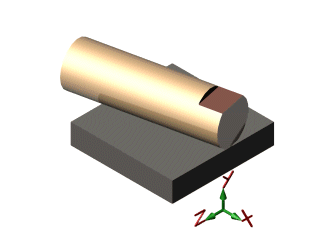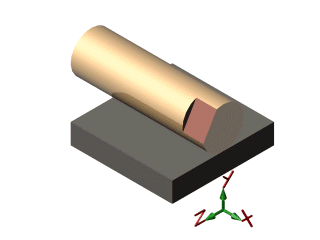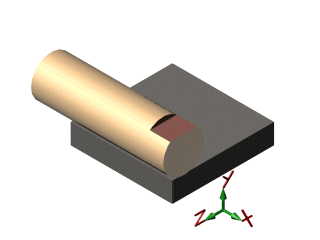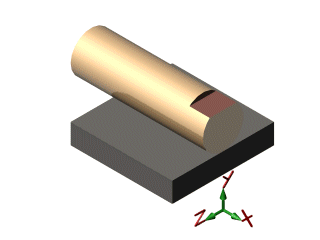Tx = 1 Rx = 1 Ty = 0 Ry = 1 Tz = 1 Rz = 0
sphère / cylindre		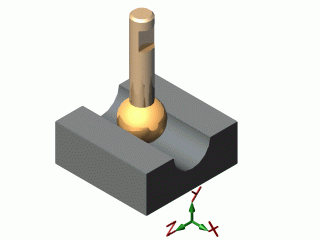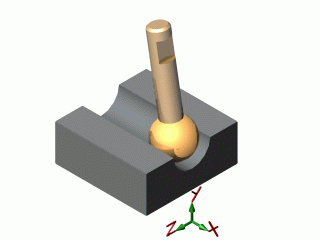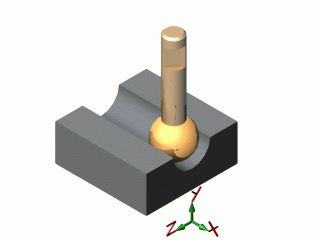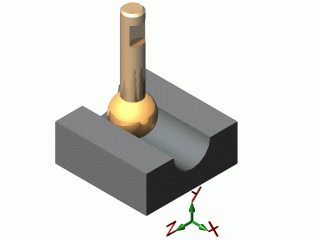Tx = 1 Rx = 1 Ty = 0 Ry = 1 Tz = 0 Rz = 1
rotule à doigt		Tx = 0 Rx = 0 Ty = 0 Ry = 1 Tz = 0 Rz = 1
hélicoïdale		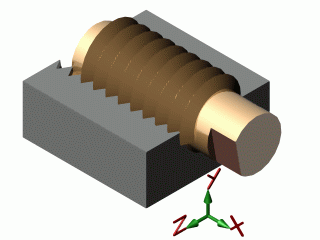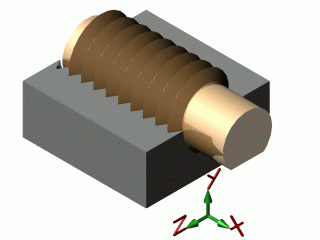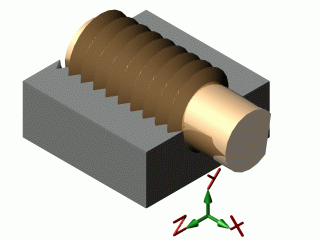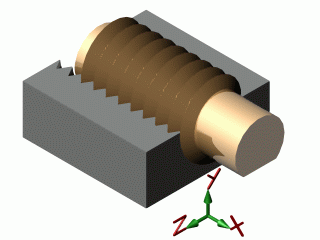Tx = 1 Rx = 1 * Ty = 0 Ry = 0 Tz = 0 Rz = 0 * Rx et Tx liées : Rx = Tx.2π /p p : pas

La liaison hélicoïdale autorise 2 mouvements mais liés (une rotation et une translation dépendantes). Elle ne possède donc qu'un seul degré de liberté (et non 2 degrés de liberté indépendants), mais elle interdit bien 2 rotations et 2 translations.

Si on classe les 10 liaisons de base (sans la liaison hélicoïdale qui est particulière) en fonction de leur degré de liberté on s'aperçoit qu'il n'y a jamais plus de 2 liaisons dans chaque catégorie :

• combien de liaisons possèdent 0 ou 5 degrés de liberté ? Une seule liaison dans chaque cas
• combien de liaisons possèdent 1, 2, 3 ou 4 degrés de liberté ? Exactement 2 liaisons dans chaque cas
• combien de liaisons possède 6 degrés de liberté ? Aucune liaison dans ce cas

Classement des 10 liaisons cinématiques de base en fonction de leurs degrés de liberté
Nombre de degrés de liberté	Nombre de degrés de liaison	Liaisons correspondantes
0	6	encastrement
1	5	glissière pivot
2	4	pivot glissant rotule à doigt
3	3	appui plan rotule
4	2	cylindre / plan sphère / cylindre
5	1	sphère / plan
6	0	aucune

Classons maintenant les 10 liaisons de base en fonction du nombre de rotations autorisées :

• combien de liaisons autorisent 0 ou 2 rotations ? Exactement 2 liaisons dans chaque cas
• combien de liaisons autorisent 1 ou 3 rotations ? Exactement 3 liaisons dans chaque cas

Classement des 10 liaisons cinématiques de base en fonction des rotations autorisées
Nombre de rotations autorisées	Nombre de rotations interdites	Liaisons correspondantes
0	3	encastrement glissière
1	2	pivot pivot glissant appui plan
2	1	cylindre / plan rotule à doigt
3	0	rotule sphère / plan sphère / cylindre

Enfin si on classe les 10 liaisons de base en fonction du nombre de translations autorisées on obtient :

• combien de liaisons autorisent 0 translation ? Il y a 4 liaisons dans ce cas
• combien de liaisons autorisent 1 ou 2 translations ? Exactement 3 liaisons dans chaque cas
• combien de liaisons autorisent 3 translations ? Aucune liaison dans ce cas

Classement des 10 liaisons cinématiques de base en fonction des translations autorisées
Nombre de translations autorisées	Nombre de translations interdites	Liaisons correspondantes
0	3	encastrement pivot rotule rotule à doigt
1	2	glissière pivot glissant sphère / cylindre
2	1	appui plan sphère / plan cylindre / plan
3	0	aucune

Remarque : sur les 11 liaisons cinématiques, 4 ont un nom universel et unique (glissière, pivot, pivot glissant et hélicoïdale), mais les 7 autres possèdent un second nom à connaître et strictement équivalent au nom d'origine :

Les 7 liaisons cinématiques qui portent 2 noms
Nom d'origine	Autre nom équivalent à connaître
encastrement	complète (ou fixe)
appui plan	plane
rotule	sphérique
sphère / plan	ponctuelle
cylindre / plan	linéaire rectiligne
sphère / cylindre	linéaire annulaire
rotule à doigt	sphérique à doigt

Certains noms sont plus proche de la forme géométrique des pièces alors que d'autres rappelent parfois plus la nature de leur surface de contact.

Il existe 3 types de contact entre deux solides S1 et S2 :

• Contact ponctuel : S1 et S2 sont en contact ponctuel si l’intersection de leur représentation géométrique est un point. Exemple : contact Sphère / Plan
• Contact linéique : S1 et S2 sont en contact linéique si l’intersection de leur représentation géométrique est une ligne :
      - une ligne droite : Contact linéique rectiligne. Exmple : Cylindre / Plan
      - un cercle ou arc de cercle : Contact linéique annulaire. Exemple : Sphère / Cylindre
• Contact surfacique : S1 et S2 sont en contact surfacique si l’intersection de leur représentation géométrique est une surface. Exemple : Plan / Plan

Voici les symboles des 11 liaisons cinématiques :

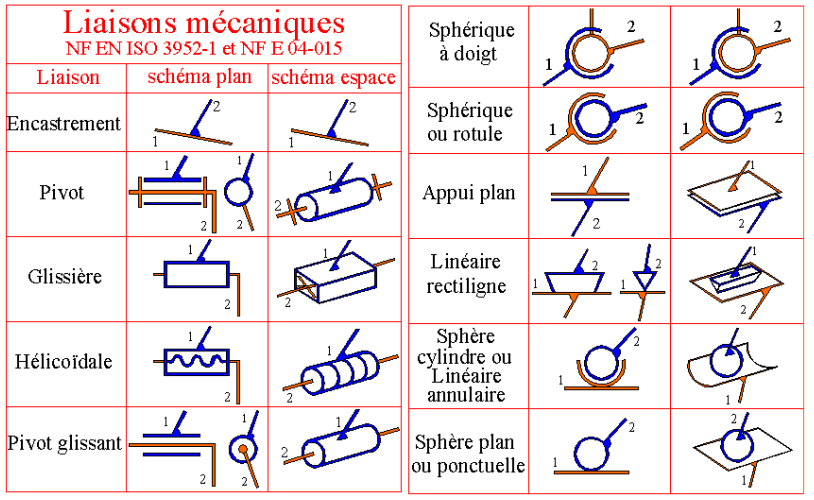
Enfin, un solide en liberté dans l'espace, sans contact avec un autre solide, possède 6 degrés de liberté (et 0 degré de liaison). On parle alors de liaison nulle (ou libre), qui pourrait constituer une 12^ème liaison cinématique (mais particulière car liée à une seule pièce, et sans aucun contact).

 

Retour au sommaire

Ce paragraphe décrit les mécanismes de transmission ou de transformation du mouvement les plus utilisés, en se limitant au principe de base et sans entrer dans les détails techniques de conception. Une recherche sur Internet permet d'obtenir rapidement des informations complémentaires.

La transformation du mouvement est une fonction mécanique complexe qui consiste à transmettre un mouvement d'une pièce à une autre, tout en modifiant sa nature. Le type de mouvement change, soit d'un mouvement de rotation à un mouvement de translation ou inversement.

 

Les engrenages

Les engrenages sont des systèmes mécaniques qui permettent la transformation d’un mouvement de rotation en un autre mouvement de rotation, les deux rotations s’effectuant autour d’axes fixes l’un par rapport à l’autre. Ces axes peuvent être parallèles, concourants ou quelconques. Chargés de transmettre à l’arbre d’entrée du système récepteur l’énergie disponible sur un «axe moteur», les engrenages doivent résister aux brusques variations de régime et fonctionner de telle sorte que les vitesses angulaires des deux arbres restent dans un rapport constant.

Dans la transmission du mouvement, pour éviter le glissement, nous utilisons des roues dentées. L’ensemble de deux roues dentées est nommé engrenage. Quand deux roues dentées sont en prise, la petite s’appelle le pignon et la grande conserve le nom de roue.

Lorsqu'une roue tourne chaque dent cette roue fait avancer l'autre roue d'une dent en l'entraînant dans le sens inverse. Si les deux roues dentées composant l'engrenage n'ont pas le même nombre de dents alors les roues ne tourneront pas à la même vitesse :

La roue qui transmet l'énergie mécanique à l'autre est appelée la roue menante, et la roue qui est entraînée par la roue menante est appelée la roue menée.

On appelle rapport de transmission (noté R et appelé aussi rapport de réduction) le rapport de la vitesse angulaire de sortie sur la vitesse angulaire d’entrée, soit aussi nombre de dents de l’entrée (appelé la roue menante) sur le nombre de dents de la sortie (appelé la roue menée) de l’engrenage. Si R est supérieur à 1 on parle de multiplicateur, si R est inférieur à 1 on parle de réducteur.

Prenons par exemple l'engrenage suivant où la roue 1 (le pignon) a 16 dents et la roue 2 possède 24 dents :

On note Z le nombre de dents de chaque roue dentée : Z₁=16 et Z₂=24

La roue 2 tournera toujours moins vite que le pignon car elle a plus de dents : si le pignon fait 1 tour alors la roue 2 avance de 16 dents, soit moins qu'un tour. Le rapport de transmission dépend de la roue menante, c'est à dire de la roue qui va entraîner l'autre :

• si la roue menante est la roue 1 alors le rapport de transmission est Z₁ / Z₂ = 16/24 = 2/3 = 0.666 soit un rapport de transmission inférieur à 1, ce qui veut dire que la roue menée (la roue 2) tourne moins vite que la roue menante (la roue 1)

• si la roue menante est la roue 2 alors le rapport de transmission est Z₂ / Z₁ = 24/16 = 3/2 = 1.5 soit un rapport de transmission supérieur à 1, ce qui veut dire que la roue menée (la roue 1) tourne plus vite que la roue menante (la roue 2)

Le rapport de transmission correspond au rapport des vitesses angulaires. On note N₁ la vitesse angulaire de la roue 1 (en radian par seconde) et N₂ la vitesse angulaire de la roue 2 (en radian par seconde). Le rapport de transmission R dépend de la roue menante :

• si la roue menante est la roue 1 alors R = Z₁ / Z₂ = N₂ / N₁

• si la roue menante est la roue 2 alors R = Z₂ / Z₁ = N₁ / N₂

Remarque : la vitesse angulaire des roues en radian par seconde peut être remplacée par la fréquence de rotation des roues exprimée en tour par seconde ou en tour par minute.

Dans tous les cas on retiendra que :

R = Z_E / Z_S = N_S / N_E

 

où E signifie l'entrée, soit la roue menante, et S représente la sortie, soit la roue menée :

E → menante

S → menée

Pour calculer le rapport de transmission d'un engrenage il faut donc préciser où est l'entrée et où est la sortie, ce qui revient à préciser qui est la roue menante (l'entrée).

Question : quel est le rapport de transmission de l'engrenage animé ci-dessous dans lequel la roue jaune a 8 dents et la roue rouge a 16 dents ?

Réponse : ça dépend de la roue menante. Si la roue menante est la jaune alos R=0.5, mais si la roue menante est la rouge alors R=2.

Exemple d'engrenages

Rapport de transmission d'un train d'engrenages :

Un train d’engrenages est une combinaison de plusieurs engrenages.

Exemple 1 dans lequel la roue menante est la roue 1 :

 

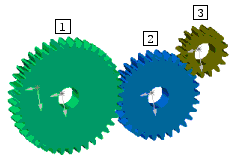
Si la roue 1 avance d'une dent, alors la roue 3 avancera aussi d'une dent quel que soit le nombre de dents de la roue intermédiaire n°2. On en déduit que le rapport de transmission de ce train d'engrenages est R = Z₁ / Z₃.

 

Exemple 2 dans lequel la roue menante est la roue 1 :

 

Si la roue 1 en entrée avance d'une dent, alors la roue 6 en sortie avancera aussi d'une dent quel que soit le nombre de dents des roues intermédiaires 2 3 4 et 5 . On en déduit que le rapport de transmission total de ce train d'engrenages est R = Z₁ / Z₆ et qu'il ne dépend ni de Z₂, ni de Z₃, ni de Z₄, ni de Z₅.

 

Exemple 3 dans lequel la roue menante est la roue 1 :

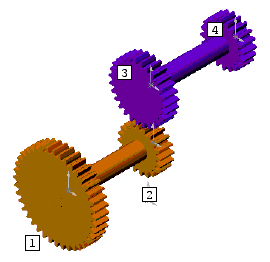
Ici les roues 1 et 2 tournent exactement à la même vitesse, et les roues 3 et 4 tournent également à la même vitesse.

Le rapport de transmission qui se calcule uniquement avec les roues dentées qui sont en contact est R = Z₂ / Z₃.

 

Exemple 4 dans lequel la roue menante est la roue 1 :

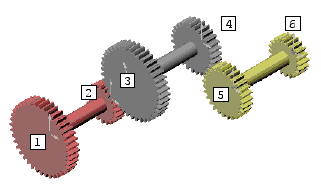
Ici on a 2 contacts entre des roues dentées (2 et 3 puis 4 et 5), soit 2 rapports de transmission intermédiaires. Le rapport de transmission total du train d'engrenages est alors égal au produit de chacun des rapports, soit R = (Z₂ / Z₃).(Z₄ / Z₅) = (Z₂.Z₄).(Z₃.Z₅).

Entre les roues 2 et 3 la roue menante est la roue 2 et entre les roues 4 et 5 la roue menante est la roue 4. On en déduit que pour ce type de train d'engrenages le rapport de transmission total est égal au produit des nombres de dents des roues menantes divisé par le produit des nombres de dents des roues menées :

 

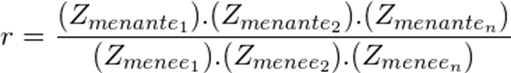
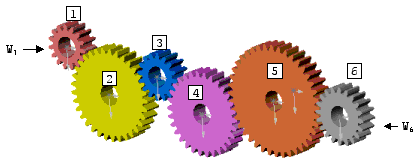
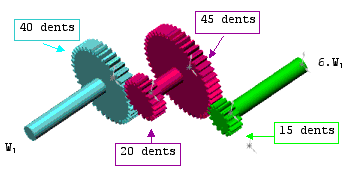
Exemple 5 dans lequel la roue menante est la roue bleue :

Le rapport de transmission total est égal au produit des nombres de dents des roues menantes divisé par le produit des nombres de dents des roues menées soit :

R = (40*45)/(20*15) = 40/20 * 45/15 = 2*3 = 6

On en déduit que la roue verte tourne 6 fois plus vide que la roue bleue.

Exemple de train d'engrenages

 

Poulie/courroie

Une courroie est un lien flexible destiné à assurer une transmission de puissance entre un arbre moteur et un arbre récepteur dont les axes peuvent occuper diverses positions relatives.

 

La vis sans fin

Une vis sans fin est un cylindre comportant une ou plusieurs cannelures hélicoïdales. Associée à une roue dentée, elle constitue un engrenage gauche (c'est-à-dire un engrenage dans lequel les axes des deux roues dentées ne sont pas dans le même plan), dans lequel elle se comporte comme une roue à n dent (n étant le nombre de cannelures). On appelle aussi ce système roue et vis sans fin.

 

Pignon/crémaillère

Le système à pignon et crémaillère transforme le mouvement de rotation du pignon en un mouvement de translation de la crémaillère ou vice versa.

Une crémaillère est une barre garnie de dents. D’un point de vue mathématique, elle peut être assimilé à une roue dentée de diamètre infini.

Ce système comprend une roue dentée qu’on appelle « pignon » et une tige dentée qu’on appelle « crémaillère ». Lorsque le pignon tourne, ses dents s’engrènent dans les dents de la crémaillère et entraînent cette dernière dans un mouvement de translation. À l’inverse, si l’on fait bouger la crémaillère, les dents de la crémaillère s’engrèneront dans les dents du pignon qui subira alors un mouvement de rotation. Il s'agit donc d'un système réversible.

 

La came

Une came est une pièce tournante, généralement disque non circulaire à saillie ou encoche, servant à transformer un mouvement de rotation en un mouvement de translation. La pièce en contact avec le profil de la came, le suiveur, est alors mise en mouvement.

Le système de came et tige-poussoir (aussi appelée tige guidée) permet de transformer le mouvement de rotation de la came en un mouvement de translation alternatif (de va-et-vient) de la tige-poussoir.

On appelle «came» une roue qui a la forme d’un œuf. La came peut aussi être un disque de forme irrégulière ou un disque dont le pivot est décentré. Dans ce cas, on parle d'«excentrique». On appelle «tige-poussoir» ou «tige guidée» la tige qui est appuyée sur la came. Lorsque la came tourne, la tige-poussoir effectue un mouvement de translation alternatif (mouvement de va-et-vient rectiligne). Ce système est irréversible.

La pièce animée d'un mouvement de rotation est appelée la came et la pièce est animée d'un mouvement de translation est appelée le piston :

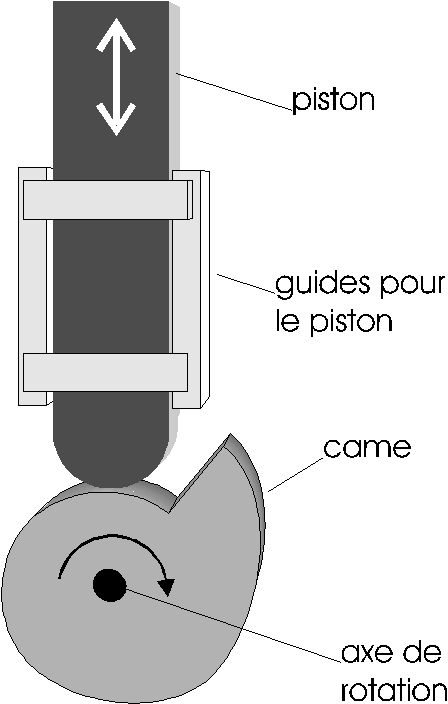
Voici un exemple de mécanisme en mouvement :

Exemple de came

 

Bielle manivelle

Le mécanisme bielle manivelle est destiné à transformer un mouvement rectiligne alternatif en un mouvement circulaire continu (machine à vapeur, moteur à combustion interne) ou inversement (pompe à piston, étau-limeur, scie alternative).

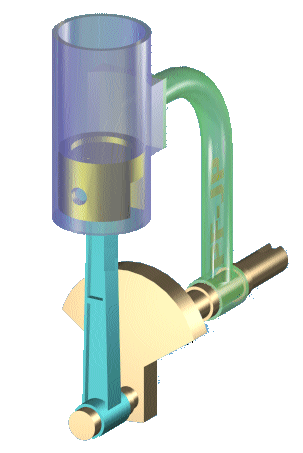
Une pièce est animée d'un mouvement de rotation (appelée la manivelle), une pièce est animée d'un mouvement de translation (appelée le piston), et la pièce qui transmet le mouvement entre la manivelle et le piston est appelée la bielle :

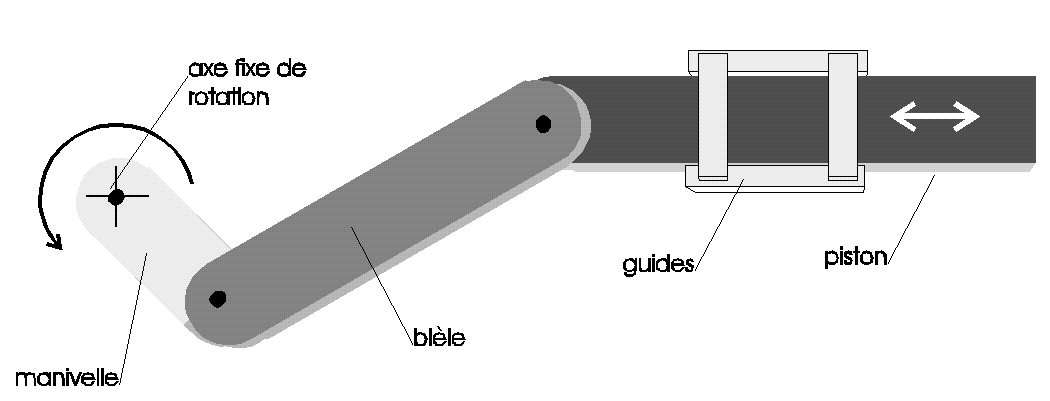
Dans le système bielle-manivelle, on distingue le bâti (partie fixe guidant le piston appelé "guides" ci-dessus), la manivelle, la bielle, et le piston. La manivelle est liée au bâti par une articulation rotoïde (perpendiculaire au plan de la figure ci-dessus), la bielle est liée à la manivelle par une articulation rotoïde (son mouvement par rapport au bâti est un mouvement plan sur plan), le piston est lié à la bielle par une articulation rotoïde (le mouvement du piston par rapport au bâti est un mouvement de translation rectiligne). On peut dire que cette chaîne des trois solides (la manivelle, la bielle et le piston) a un degré de liberté par rapport au bâti.

Voici un exemple de mécanisme en mouvement :

Exemple de bielle manivelle

Le système à bielle et manivelle transforme un mouvement de rotation en mouvement de translation alternatif (mouvement de va-et-vient rectiligne) et vice versa.

Dans ce système, la bielle est la tige rigide liée par une liaison pivot à ses deux extrémités alors que la partie «manivelle» représente la pièce sur laquelle on peut appliquer un mouvement de rotation. Le contact entre la bielle et la manivelle est essentiel afin que le mouvement puisse être transmis dans le système. Le mouvement est généralement initié par la rotation de la manivelle qui transmet un mouvement de translation alternatif à la bielle. Cette transformation est réversible puisqu'elle peut s'effectuer dans le sens inverse.

Il est à noter que la bielle, parfois organe récepteur, peut aussi être un organe intermédiaire qui transmettra le mouvement de translation à une autre pièce, par exemple à un piston. Dans un moteur à combustion, le système à bielle et à manivelle occupe une place importante. Le piston est relié à la bielle qui elle est reliée à la manivelle qui entraînera le vilebrequin. Ainsi, en remontant, le piston comprime le mélange de gaz dans le cylindre.

Retour au sommaire

La dynamique est la partie de la mécanique qui étudie les mouvements des solides en relation avec les forces qui les produisent. L'étude et la compréhension de la dynamique suppose l'aquisition des connaissances abordées en cinématique.

La cinématique étudie les mouvements sans les forces : elle nous donne les équations horaires (position, vitesse et accélération en fonction du temps) aussi bien en translation qu'en rotation.

La statique étudie les forces sans le mouvement : elle nous donne la notion de résultante des forces et de moment résultant, ainsi que le principe fondamental de la statique (un solide est immobile si son torseur des actions mécaniques est nul).

La dynamique étudie le lien entre le mouvement et les forces, la force étant une des conséquences du mouvement :

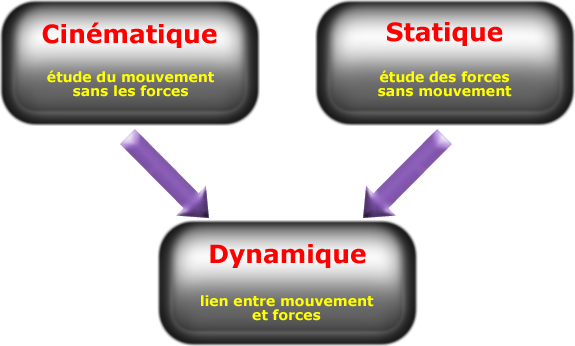
La dynamique introduit la notion d’effort s’exerçant sur un ensemble mécanique. Son but est de relier les efforts aux mouvements possibles de cet ensemble (en permettant de calculer les efforts, si l’on connaît le mouvement, ou, inversement, de déterminer le mouvement, si les efforts sont donnés ou peuvent être éliminés pour ceux d’entre eux qui seraient inconnus a priori).

La notion d’effort est issue de l’expérience quotidienne: les contacts de l’homme avec son environnement. Au fur et à mesure du développement scientifique des conceptions mécaniques, on est arrivé à unifier la notion d’effort de contact et la notion d’action à distance en les regroupant dans un même concept.

Ces notions, relativement vagues, doivent être précisées à l’aide de principes qui, dans l’état actuel de la science classique, résument et idéalisent les propriétés générales que nous attribuons à la notion d’effort d’interaction entre ensembles matériels: association d’un torseur à des efforts exercés par un ensemble matériel sur un autre ensemble matériel, principe de réception (le torseur d’action sur une réunion est la somme des torseurs d’action sur chacun des éléments), principe de génération (le torseur d’action d’une réunion sur un ensemble est la somme des torseurs d’action de chacun des éléments sur cet ensemble). Parmi tous les efforts s’exerçant sur un ensemble matériel déterminé, le mécanicien est amené à établir une distinction entre les «efforts extérieurs» à l’ensemble matériel considéré (efforts exercés par le reste de l’Univers sur cet ensemble) et les «efforts intérieurs» (efforts exercés par les éléments de l’ensemble les uns sur les autres).

 

Énergétique

En mécanique il existe 2 types d'énergie (en Joule) : l'énergie potentielle et l'énergie cinétique. Dans le cas d'un travail (en Joule) effectué par des forces engendrées par un ressort ou par la force de pesenteur on parle d'énergie potentielle. Dans ce cas le travail dépend seulement des positions initiale et finale des forces et ne dépend pas de la trajectoire. Quant à l'énergie cinétique elle est liée à la vitesse de déplacement du solide : plus un solide se déplace rapidement, plus il accumule de l'énergie cinétique. L'énergie cinétique peut être vue comme une énergie potentielle liée à la vitesse (et non à la position). Dans tous les cas l'énergie mécanique totale est égale à la somme de l'énergie cinétique et de l'énergie potentielle :

énegie mécanique = énergie cinétique + énergie potentielle

Dans toutes les transformations variées qui sont étudiées en physique, la notion d’énergie joue un rôle fondamental. Elle apparaît d’abord en mécanique, où elle signifie capacité de travail. La première forme d’énergie définie est le travail mécanique : produit scalaire d’une force et d’un déplacement. Un système mécanique pouvant fournir du travail contient du travail en réserve, c’est-à-dire de l’énergie :

• énergie potentielle si elle est due à la position des constituants du système dans l’espace
• énergie cinétique si le corps est en mouvement (pour mouvoir un bateau à voile, on utilise l’énergie cinétique des masses d’air en mouvement)

La loi de conservation de l’énergie domine la physique. Cette loi est vérifiée dans les phénomènes purement mécaniques pour la somme de l’énergie potentielle et de l’énergie cinétique. Cependant, elle semble mise en défaut chaque fois qu’il y a frottement et apparition de chaleur. Pour conserver l’énergie totale d’un système, il faut lui ajouter la quantité de chaleur reçue. La chaleur apparaît alors comme une forme de l’énergie. La thermodynamique étudie plus particulièrement les transformations de chaleur en travail et réciproquement. En réalité, la chaleur n’est pas autre chose que l’énergie cinétique d’agitation des particules qui composent le système.

 

La dynamique du point

En plus de la position, de la vitesse, et de l'accélération, en dynamique nous allons ajouter les notions de quantité de mouvement et de force (la force étant la dérivée de la quantité de mouvement).

 

La dynamique du solide

Notion de moment d'inertie J=m.l²

Le moment d'inertie est une grandeur physique qui caractérise la géométrie des masses d'un solide, c'est-à-dire la répartition de la matière en son sein. Il quantifie également la résistance à une mise en rotation de ce solide (ou plus généralement à une accélération angulaire), et se mesure en kilogramme mètre carré (le produit d'une masse et du carré d'une longueur, qui s'exprime en kg·m² dans le système international d'unités). C'est l'analogue pour un solide de la masse inertielle qui, elle, mesure la résistance d'un corps soumis à une accélération linéaire. Dans le cas simple de la rotation d'une masse autour d'un axe fixe, le moment d'inertie par rapport à cet axe est une grandeur scalaire qui apparaît dans les expressions du moment cinétique et de l'énergie cinétique de rotation de ce corps.

En translation :

quantité de mouvement = masse x vitesse linéaire

force = masse x accélération linéaire

En rotation :

moment d'inertie = masse x distance au carré

moment = moment d'inertie x accélération angulaire

 

 

Principe fondalemental de la statique (PFS), appelé aussi première loi de Newton :

Le vecteur vitesse du centre d'inertie d'un système est constant si et seulement si la somme vectorielle des forces qui s'exercent sur le système est égale au vecteur nul.

Cas général :

Théorème de la résultante statique : somme des forces = zéro

Théorème du moment statique : somme des moments = zéro

Principe fondamental de la statique : torseur des actions mécaniques externes égale au torseur nul

Enoncé du principe fondamental de la statique :

Un solide en équilibre sous l'action de n torseurs d'actions mécaniques reste en équilibre si la somme des n torseurs tous écrits au même point est égale au torseur nul.

 

Cas particulier d'un solide soumis à 2 forces :

Un solide soumis à 2 forces est en équilibre si :

• la somme vectorielle des forces est nulle
• et si les 2 forces ont même support

Cas particulier d'un solide soumis à 3 forces :

Un solide soumis à 3 forces est en équilibre si :

• la somme vectorielle des forces est nulle
• et si les 3 forces sont concourantes et coplanaires

Les 3 forces sont concourantes si leurs 3 supports se coupent en un même point.

Principe fondalemental de la dynamique (PFD), appelé aussi deuxième loi de Newton :

Théorème de la résultante dynamique : somme des forces = masse x accélération

Théorème du moment dynamique : somme des moments = moment d'inertie x accélération angulaire

Cas particulier en translation : le torseur dynamique est un torseur glisseur (moment dynamique nul)

Cas particulier en rotation : le torseur dynamique est un torseur couple (résultante dynamique nulle)

La somme des forces extérieures appliquées à un système en translation dans un référentiel Galiléen est égale à la dérivée du vecteur quantité de mouvement du centre d'inertie de ce système.

Principe des actions réciproques (ou principe des actions mutuelles), appelé aussi troisième loi de Newton :

Tout corps A exerçant une force sur un corps B subit une force d'intensité égale, de même direction mais de sens oposé, exercé par le corps B.

Livre de mécanique