Les nombres premiers

Les nombres premiers

Introduction

Je ne sais pas pour vous, mais en observant les nombres premiers, j'éprouve le sentiment d'être en présence d'un des plus inexplicables secrets de la création.

Les nombres premiers, ces nombres sans autres facteurs qu'un et eux-mêmes, fascinent : 2, 3, 5, 7, 11, 13...

Alors que leur définition semble ne receler aucun mystère, on échoue à trouver une régularité quelconque dans leur succession. Connus dès les débuts de l'arithmétique, les nombres premiers ont excité la curiosité de milliers de mathématiciens. Ils sont au cœur de la science des nombres, car tout entier se décompose de façon unique en un produit de facteurs premiers. Ils sont aussi à l'origine de certains des problèmes les plus difficiles des mathématiques et ont acquis, avec les progrès de la cryptographie, une importance économique considérable.

Sommaire de cette page

Il existe une infinité de nombres premiers, démonstration

Test élémentaire de primalité

Les 999 premiers nombres premiers

Applet Java pour la recherche des nombres premiers

Les fonctions utilisées en arithmétique pour l'études des nombres premiers

Conjectures, théorèmes, et propriétés des nombres premiers

Ecart entre les nombres premiers

Les nombres premiers jumeaux

Les nombres premiers triplets et quadruplets

Convention utilisée sur cette page pour l'écriture des exposants dans les nombres :

Afin que le texte de cette page soit compatible avec le plus grand nombre de navigateurs possible, je n'est pas utilisé le style "exposant" pour l'écriture des nombres, mais j'ai utilisé l'opérateur ^ pour symboliser la fonction puissance. Exemples :

10^2 signifie 10 puissance 2, soit 100

10^6 représente un million (et non 10 millions !)

2^87 654 signifie "2 élevé à la puissance 87 654" (et non 2 fois 10 puissance 87 654 !!!)

Un dernier exemple :

7^2 = 7 puissance 2 = 7 exposant 2 = 7 au carré = 7 fois 7 = 49

Donc rappelez vous : le ^ représente l'opérateur puissance, et non "10 exposant" comme c'est le cas sur certaines calculatrices. Le symbole ^ remplace simplement l'écriture en exposant.

Rappel au sujet de la priorité des opérateurs mathématiques, afin de chasser toute ambiguïté à la lecture des expressions complexes formulées sur cette page : l'opérateur puissance est prioritaire devant la multiplication, ce qui signifie que A^BC = A^B.C = (A^B).C et que A^BC est différent de A^(BC), avec A^(BC) = (A^B)^C = (A^C)^B

Il existe une infinité de nombres premiers, démonstration :

Démonstration claire et détaillée :

Supposons que p est un nombre premier, avec p>5, et formons le produit 2x3x5x......xp de TOUS les nombres premiers compris entre 2 et p, puis posons n=(2x3x5x......xp)+1

n étant supérieur à 2, n admet un diviseur premier. Notons-le q. Or, aucun des nombres de la liste 2, 3, 5, ...... p, n'est un diviseur de n car le reste de la division de n par l'un quelconque des nombres premiers de cette liste est toujours 1. Donc q est strictement supérieur à p.

On en déduit que quelque soit le nombre premier p, il existera toujours un autre nombre premier q supérieur à p, ce qui prouve que la liste des nombres premiers est infinie.

Remarque : le produit 2x3x5x......xp de tous les nombres premiers inférieur ou égaux au nombre premier p est appelé la primorielle de P, et est noté P#.

Et voici maintenant la même démonstration, mais que j'ai condensée au maximum, et tournée en une démonstation par l'absurde en une seule phrase :

S'il y avait un nombre fini de nombres premiers, alors le plus grand d'entre eux, p, serait tel que p# + 1 serait divisible par un nombre premier qui, divisant p#, devrait aussi diviser 1, ce qui est absurde.

On en déduit que l'ensemble des nombres premiers ne peut pas être fini, c'est à dire qu'il existe obligatoirement une infinité de nombre premiers.

Retour en haut de la page

Test élémentaire de primalité :

Un test de primalité permet de savoir si un nombre entier est un nombre premier ou pas. Il existe différentes méthodes pour tester la primalité d'un entier naturel. Un des algorithmes possibles est le suivant. Il permet de savoir rapidement si un nombre entier p, impair et supérieur à 2, est un nombre premier ou pas :

A=3

Début

si A>=sqrt(p)+1 alors p est premier

si p est un multiple de A alors p n'est pas premier

A=A+2

Retourner au début

Explications et mise en pratique de cet algorithme :

La variable A est initialisée à 3, puis elle est incrémentée de 2 à chaque passage dans la boucle. Cette variable A va donc "balayer" tous les nombres impairs en partant de 3. Si le nombre p que l'on teste est à un moment multiple de A, alors p n'est pas premier et on sort du programme. Si en revanche, la variable A atteind une valeur supérieure à la racine carrée de p, plus 1, alors p est un nombre premier et on sort du programme.

Programmation de ce test de primalité :

Dans les lignes ci-dessus, la fonction sqrt représente la fonction racine carrée, et peut être calculée de différentes manières selon les fonctions mathématiques dont on dispose :

racine carrée de p = sqrt(p) = p puissance 0,5 = exponentielle(ln(p)/2) = etc ...

Le second test, "p est un multiple de A", peut être traduit de différentes manières, toutes équivalentes :

p est un multiple de A <=> A est un diviseur de p <=> p modulo A = 0 <=> la partie décimal du nombre p/A est nulle <=> p/A est égal à sa partie entière <=> etc ...

Ces multiples possibilités permettent de programmer facilement ce test élémentaire de primalité dans tous les langages de programmation existants, aussi bien sur un ordinateur (en C, en Java, en Pascal, en Perl, etc.) que sur une calculatrice (Casio, TI, HP, etc.). Si vous réalisez vous-même votre programme de test de primalité en utilisant l'algorithme ci-dessus, n'oubliez pas que p doit être un nombre impair supérieur à 2 : il faut donc traiter à part les cas particuliers des nombres pairs, du nombre 1, et du nombre 2, avant de lancer la boucle de test :

si p est pair alors p n'est pas premier

si p=1 alors p n'est pas premier

si p=2 alors p est premier

Rappel : 1 n'est pas premier, et 2 est le seul nombre premier pair

Remarquez que le test "p est pair" peut se traduire "p est un multiple de 2", qui, comme on l'a vu, peut se programmer de différentes manières en fonction des différentes fonctions mathématiques disponibles dans le langage utilisé.

Programmation du test de primalité en Java :

Voici par exemple une applet Java que j'ai réalisée en utilisant l'algorithme de primalité décrit ci-dessus. Pour savoir si un nombre entier (à 7 chiffres maximum) est premier, entrez le nombre sur la ligne de saisie puis appuyez sur le bouton "Tester le nombre" :

Pour télécharcher le code source en Java de cette applet, cliquez ici.

Programmation du test de primalité en JavaScript :

Et voici par exemple un programme en JavaSript permettant de tester la primalité d'un nombre entier naturel p :

<SCRIPT LANGUAGE="JavaScript">
///////////////////////////////////////////////////////////////////////
// Script réalisé par Jean-Christophe MICHEL
// Juillet 2012
// www.gecif.net
///////////////////////////////////////////////////////////////////////
function VerifForm()
{
formulaire = document.forms[0];
p = formulaire.nombre.value;
a = 3;
sortir=0;
var exp=new RegExp("^[0-9]*$","g"); // teste si p ne contient que des chiffres (élimine les lettres, la virgule, le signe -, etc.)
if ( !exp.test(p) )
{
document.getElementById('targetDiv').innerHTML ="Entrez un nombre entier strictement positif";
sortir=1;
}
else
if (p<1)
{ // cas où p=0
document.getElementById('targetDiv').innerHTML ="Entrez un nombre entier strictement positif";
sortir=1;
}
else
if (p==2) { // cas où p=2
document.getElementById('targetDiv').innerHTML =p + " est un nombre premier"; sortir=1;
}
else
if (p==1)
{ // cas où p=1
document.getElementById('targetDiv').innerHTML =p + " n'est pas un nombre premier";
sortir=1;
}
else
if (p % 2==0)
{ // cas où p est pair
document.getElementById('targetDiv').innerHTML =p + " n'est pas un nombre premier";
sortir=1;
}
while (sortir==0)
{
if (a>=(Math.sqrt(p)+1))
{
document.getElementById('targetDiv').innerHTML =p + " est un nombre premier";
sortir=1;
}
else
if (p % a==0)
{
document.getElementById('targetDiv').innerHTML =p + " n'est pas un nombre premier";
sortir=1;
}
a=a+2;
}
}
</SCRIPT>

Cliquez ici pour tester ce programme dans une nouvelle page.

Retour en haut de la page

Les 999 premiers nombres premiers :

Ce tableau, de 10 colonnes et 100 lignes, contient les 999 premiers nombres premiers. A titre d'information, la somme de ces 999 nombres est 3 678 910 (remarquez la suite de nombres 6 7 8 9 10 dans cette somme) :

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997	1009	1013
1019	1021	1031	1033	1039	1049	1051	1061	1063	1069
1087	1091	1093	1097	1103	1109	1117	1123	1129	1151
1153	1163	1171	1181	1187	1193	1201	1213	1217	1223
1229	1231	1237	1249	1259	1277	1279	1283	1289	1291	1297
1301	1303	1307	1319	1321	1327	1361	1367	1373	1381
1399	1409	1423	1427	1429	1433	1439	1447	1451	1453
1459	1471	1481	1483	1487	1489	1493	1499	1511	1523
1531	1543	1549	1553	1559	1567	1571	1579	1583	1597
1601	1607	1609	1613	1619	1621	1627	1637	1657	1663
1667	1669	1693	1697	1699	1709	1721	1723	1733	1741
1747	1753	1759	1777	1783	1787	1789	1801	1811	1823
1831	1847	1861	1867	1871	1873	1877	1879	1889	1901
1907	1913	1931	1933	1949	1951	1973	1979	1987	1993
1997	1999	2003	2011	2017	2027	2029	2039	2053	2063
2069	2081	2083	2087	2089	2099	2111	2113	2129	2131
2137	2141	2143	2153	2161	2179	2203	2207	2213	2221
2237	2239	2243	2251	2267	2269	2273	2281	2287	2293
2297	2309	2311	2333	2339	2341	2347	2351	2357	2371
2377	2381	2383	2389	2393	2399	2411	2417	2423	2437
2441	2447	2459	2467	2473	2477	2503	2521	2531	2539
2543	2549	2551	2557	2579	2591	2593	2609	2617	2621
2633	2647	2657	2659	2663	2671	2677	2683	2687	2689
2693	2699	2707	2711	2713	2719	2729	2731	2741	2749
2753	2767	2777	2789	2791	2797	2801	2803	2819	2833
2837	2843	2851	2857	2861	2879	2887	2897	2903	2909
2917	2927	2939	2953	2957	2963	2969	2971	2999	3001
3011	3019	3023	3037	3041	3049	3061	3067	3079	3083
3089	3109	3119	3121	3137	3163	3167	3169	3181	3187
3191	3203	3209	3217	3221	3229	3251	3253	3257	3259
3271	3299	3301	3307	3313	3319	3323	3329	3331	3343
3347	3359	3361	3371	3373	3389	3391	3407	3413	3433
3449	3457	3461	3463	3467	3469	3491	3499	3511	3517
3527	3529	3533	3539	3541	3547	3557	3559	3571	3581
3583	3593	3607	3613	3617	3623	3631	3637	3643	3659
3671	3673	3677	3691	3697	3701	3709	3719	3727	3733
3739	3761	3767	3769	3779	3793	3797	3803	3821	3823
3833	3847	3851	3853	3863	3877	3881	3889	3907	3911
3917	3919	3923	3929	3931	3943	3947	3967	3989	4001
4003	4007	4013	4019	4021	4027	4049	4051	4057	4073
4079	4091	4093	4099	4111	4127	4129	4133	4139	4153
4157	4159	4177	4201	4211	4217	4219	4229	4231	4241
4243	4253	4259	4261	4271	4273	4283	4289	4297	4327
4337	4339	4349	4357	4363	4373	4391	4397	4409	4421
4423	4441	4447	4451	4457	4463	4481	4483	4493	4507
4513	4517	4519	4523	4547	4549	4561	4567	4583	4591
4597	4603	4621	4637	4639	4643	4649	4651	4657	4663
4673	4679	4691	4703	4721	4723	4729	4733	4751	4759
4783	4787	4789	4793	4799	4801	4813	4817	4831	4861
4871	4877	4889	4903	4909	4919	4931	4933	4937	4943
4951	4957	4967	4969	4973	4987	4993	4999	5003	5009
5011	5021	5023	5039	5051	5059	5077	5081	5087	5099
5101	5107	5113	5119	5147	5153	5167	5171	5179	5189
5197	5209	5227	5231	5233	5237	5261	5273	5279	5281
5297	5303	5309	5323	5333	5347	5351	5381	5387	5393
5399	5407	5413	5417	5419	5431	5437	5441	5443	5449
5471	5477	5479	5483	5501	5503	5507	5519	5521	5527
5531	5557	5563	5569	5573	5581	5591	5623	5639	5641
5647	5651	5653	5657	5659	5669	5683	5689	5693	5701
5711	5717	5737	5741	5743	5749	5779	5783	5791	5801
5807	5813	5821	5827	5839	5843	5849	5851	5857	5861
5867	5869	5879	5881	5897	5903	5923	5927	5939	5953
5981	5987	6007	6011	6029	6037	6043	6047	6053	6067
6073	6079	6089	6091	6101	6113	6121	6131	6133	6143
6151	6163	6173	6197	6199	6203	6211	6217	6221	6229
6247	6257	6263	6269	6271	6277	6287	6299	6301	6311
6317	6323	6329	6337	6343	6353	6359	6361	6367	6373
6379	6389	6397	6421	6427	6449	6451	6469	6473	6481
6491	6521	6529	6547	6551	6553	6563	6569	6571	6577
6581	6599	6607	6619	6637	6653	6659	6661	6673	6679
6689	6691	6701	6703	6709	6719	6733	6737	6761	6763
6779	6781	6791	6793	6803	6823	6827	6829	6833	6841
6857	6863	6869	6871	6883	6899	6907	6911	6917	6947
6949	6959	6961	6967	6971	6977	6983	6991	6997	7001
7013	7019	7027	7039	7043	7057	7069	7079	7103	7109
7121	7127	7129	7151	7159	7177	7187	7193	7207	7211
7213	7219	7229	7237	7243	7247	7253	7283	7297	7307
7309	7321	7331	7333	7349	7351	7369	7393	7411	7417
7433	7451	7457	7459	7477	7481	7487	7489	7499	7507
7517	7523	7529	7537	7541	7547	7549	7559	7561	7573
7577	7583	7589	7591	7603	7607	7621	7639	7643	7649
7669	7673	7681	7687	7691	7699	7703	7717	7723	7727
7741	7753	7757	7759	7789	7793	7817	7823	7829	7841
7853	7867	7873	7877	7879	7883	7901	7907	7919	etc.

Retour en haut de la page

Applet Java pour la recherche des nombres premiers

L'applet Java suivante vous permet de rechercher des nombres premiers. Il vous suffit d'entrer un nombre entier à 7 chiffres maximum, et en appuyant sur le bouton "Rechercher suivant", le premier nombre premier trouvé après le nombre que vous avez entré sera affiché :

Retour en haut de la page

Les fonctions utilisées en arithmétique pour l'études des nombres premiers :

La fonction d(n) :

Définition d'un diviseur :

Pour qu'un entier k soit un diviseur de n, il faut et il suffit que le reste de la division de n par k soit nul. Comme un nombre n sera toujours divisible par 1 et par n lui-même, 1 et n sont toujours des diviseurs de n. On peut donc déjà remarquer que tout entier n>1 possède au moins deux diviseurs : 1 et n lui-même.

La fonction d(n) est égale au nombre de diviseurs de n (y compris 1 et n lui-même d'après la définition d'un diviseur).

Exemples :

d(18) = 6 car 18 a 6 diviseurs, qui sont 1, 2, 3, 6, 9 et 18

d(32) = 6 car 32 a 6 diviseurs, qui sont 1, 2, 4, 8, 16 et 32

d(25) = 3 car 25 a 3 diviseurs, qui sont 1, 5 et 25

d(17) = 2 car 17 a seulement 2 diviseurs, qui sont 1+17 = 18

Un nombre n est premier s'il ne possède comme diviseurs que 1 et n lui-même, donc n est un nombre premier si et seulement si d(n)=2.

Remarque : le seul diviseur de 1 est 1 lui-même. Donc le nombre 1 ne possède qu'un seul diviseur, ce qui s'écrit d(1)=1. Comme d(1) est différent de 2, on en déduit que 1 n'est pas un nombre premier.

Retour en haut de la page

La fonction indicatrice d'Euler (Phi de n) :

La fonction indicatrice d'Euler, notée, est égale au nombre d'entiers inférieurs à n et n'ayant aucun diviseur commun avec n.

Exemple : (6) = 2 car les seuls nombres inférieurs à 6 et premiers avec lui sont 1 et 5.

Remarque : n - (n) ne pourra jamais être égal à 10.

Retour en haut de la page

La fonction Sigma de n :

est la somme de tous les diviseurs de n, y compris 1 et n lui-même.

Exemples :

(18) = 1+2+3+6+9+18 = 39

(32) = 1+2+4+8+16+32 = 63

(25) = 1+5+25 = 36

(17) = 1+17 = 18

Si (n) = 1+n, cela signifie que n n'a que 2 diviseurs : 1 et n. Dans ce cas, n est un nombre premier.

Exemple : (13) = 1+13 = 14 donc 13 est un nombre premier.

On appelle "nombre parfait" un entier dont la somme de ses diviseurs est égale au double du nombre, ce qui s'écrit :

Si (n) = 2.n alors n est un nombre parfait.

Exemple : (6) = 1+2+3+6 = 12 = 2x6, donc 6 est un nombre parfait.

Les six premiers nombres parfaits sont :

6
28
496
8 128
33 550 336
8 589 869 056

Jusqu'à présent, aucun nombre parfait impair n'a été découvert. Mais cela ne veut pas dire qu'un nombre parfait est forcément pair. Alors cherchez bien, et si vous trouvez un nombre parfait impair, faites-moi signe :-))

Retour en haut de la page

La fonction Pi de x :

La fonction , définie pour tout nombre réel x > 0, correspond au nombre de nombres premiers inférieurs ou égaux à x.

Exemples :

(6) = 3 car il existe 3 nombres premiers inférieurs ou égaux à 6 : 2, 3, et 5

(11) = 5 car il existe 5 nombres premiers inférieurs ou égaux à 11 : 2, 3, 5, 7, et 11

(21.13) = 8 car il existe 8 nombres premiers inférieurs ou égaux à 21.13 : 2, 3, 5, 7, 11, 13, 17 et 19

(1) = 0 car il n'existe aucun nombre premier inférieur ou égal à 1 (1 n'étant pas un nombre premier)

(2) = 1 car il n'existe qu'un seul nombre premier inférieur ou égal à 2 : c'est 2 lui-même

Le tableau ci-dessus donnant les 999 premiers nombres premiers permet d'obtenir facilement la valeur de la fonction (x). Par exemple, combien vaut (100) ? Grâce au tableau, on s'aperçoit qu'il existe 25 nombres premiers inférieurs ou égaux à 100 (il y a 10 nombres par ligne dans le tableau). On en déduit donc que (100) = 25

Remarque : bien que cette fonction Pi de x soit représentée par la même lettre grecque que le nombre Pi de valeur 3.141592..., la fonction (x) n'a aucun rapport avec le nombre réel de valeur 3.141592... Ce n'est qu'un hasard dans l'attribution des noms, qui fait que ces deux éléments mathématiques sont représentés par la même lettre. Cette remarque est d'autant plus importante lorsqu'on utilise des formules (et il y en a) qui font intervenir à la fois la fonction (x) et le nombre réel .

Retour en haut de la page

La fonction Primorielle :

La fonction primorielle de p, notée p#, n'est définie que si p est un nombre premier.

p# désigne alors le produit de tous les nombres premiers inférieurs ou égaux à p.

Exemple :

5# = 2x3x5 = 30

11# = 2x3x5x7x11 = 2 310

17# = 2x3x5x7x11x13x17 = 510 510

23# = 2x3x5x7x11x13x17x19x23 = 223 092 870

2# = 2

6# n'existe pas car 6 n'est pas un nombre premier.

Le premier nombre premier étant 2, le produit p# commencera toujours par 2. On en déduit que p# sera toujours pair, quelque soit le nombre premier p.

Utilisation de la fonction primorielle :

Quelle est le plus petit entier ayant 3 diviseurs premiers distincts ? La réponse est primorielle de 5 (notée 5#) :

5#=2x3x5=30 donc 30 est le plus petit entier ayant trois diviseurs premiers distincts : 2, 3 et 5.

Le plus petit entier à 4 diviseurs premiers distincts est 7#=2x3x5x7=210

2310 = 11# = 2x3x5x7x11, donc 2310 est le plus petit entier à 5 diviseurs premiers distincts, etc..

La plupart des entiers ont très peu de diviseurs premiers distincts. Les primorielles sont donc des nombres exceptionnels.

Fonction primorielle et nombres premiers :

n# + 1 est premier pour n=2, 3, 5, 7, 11, 31, 379, 1019, 1021, 2657, 3229, 4547, 4787, 11549, 13649, 18523, 23801, 24029, et pour aucune autre valeur inférieure à 35000.

Propriétés de la fonction primorielle :

Les seules primorielles qui peuvent s'écrire comme étant le produit de deux nombres consécutifs sont les primorielles de 2, 3, 7, et 17 :

2# = 2 = 1x2

3# = 6 = 2x3

7# = 2x3x5x7 = 210 = 14x15

17# = 2x3x5x7x11x13x17 = 510 510 = 714x715

Il n'existe aucune autre primorielle possédant ces propriétés jusqu'à 3049#.

17# est donc égal à un produit de deux nombres consécutifs faisant intervenir 714. J'en profite pour signaler une particularité de ce nombre 714 : Avez-vous remarqué que (714) est un cube parfait, et que le rapport (714) /(714) est un carré parfait ? Connaissez-vous d'autres nombres possédant cette particularité ?

De plus, 17# est égal au produit de 4 nombres de Fibonacci consécutifs : 17# = 13x21x34x55

Décidément, quel nombre extraordinaire ce primorielle de 17 !! :-))

Retour en haut de la page

La fonction sous-factorielle :

La fonction sous-factorielle de n, notée !n, est définie de la manière suivant (où n! représente la fonction factorielle de n) :

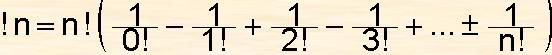
Rappel : 0! = 1

Exemple :

!0 = 0! = 1

!1 = 1! (1 - 1) = 0

!2 = 2! (1 - 1 + 1/2) = 1

!3 = 3! (1 - 1 + 1/2 - 1/6) = 2

!4 = 4! (1 - 1 + 1/2 - 1/6 + 1/24) = 9

!5 = 5! (1 - 1 + 1/2 - 1/6 + 1/24 - 1/120) = 44

!6 = 6! (1 - 1 + 1/2 - 1/6 + 1/24 - 1/120 + 1/720) = 265

etc.

On remarque que la fonction sous-factorielle est un entier positif, pour des nombres supérieur à 1 (ce que ne laissait pas forcément présager la définition de la sous-factorielle).

Exemple de problème utilisant la fonction sous-factorielle :

N lettres ont été écrites à différentes adresses et N enveloppes affranchies ont été préparées. De combien de manières les lettres peuvent-elles être placées dans les enveloppes de sorte que chaque lettre se trouve dans la mauvaise enveloppe ?

La réponse est : sous-factorielle de N

Complément d'information sur ce problème des lettres mal adressées : lorsque le nombre de lettres et d'enveloppes N augmente, la probabilité que chaque lettre soit placée dans une mauvaise enveloppe tend rapidement vers la valeur exponentielle de -1, soit :

Le même problème peut être simulé en battant bien 2 jeux de 52 cartes et en retournant les cartes par paires, une sur chaque paquet. La probabilité qu'il y ait aucune correspondance parmi les 52 paires est d'environ e^-1.

Retour en haut de la page

Quelques propriétés arithmétiques de ces fonctions :

Les valeurs de n, pour lesquelles (n) est un diviseur de (n), et d(n) est à la fois un diviseur de (n) et de (n) forment la suite : 1 3 15 30 35 52 70 78 105 140 168 190 210 etc... On peut remarquer dans cette liste la présence de 30 = 5# et de 210 = 7#.

Le premier nombre composé de la forme p# + 1 est obtenu pour p=13. Ce nombre est 2x3x5x7x11x13 + 1 = 30 031

Le seul nombre égal à la somme des sous-factorielles de ses chiffres est 148 349. En effet :

148 349 = !1 + !4 + !8 + !3 + !4 + !9

Retour en haut de la page

Conjectures, théorèmes, et propriétés des nombres premiers :

Tout nombre entier pair, supérieur à 2, est la somme de 2 nombres premiers.

Rappel : 1 n'est pas premier et 2 est le seul nombre premier pair.

Il y a exactement autant de nombres premiers de la forme 4n+1 inférieurs à 26 861 qu'il y en a de la forme 4n+3. Comme 26 861 est premier et de le forme 4n+1, il rend cette forme majoritaire, pour la première fois.

Les nombres de la forme n! - 1 sont premiers pour n=3, 4, 6, 7, 12, 14, 30, 32, 33, 38, 94, 166, 324, 379, 469, 546, 974, 1963, 3507, 3610, et il n'en existe pas d'autre jusqu'à 4580 compris.

Si 2ⁿ- 1 est premier, alors n est premier.

Pour tout nombre premier p, (p-1)! + 1 est un multiple de p.

Si p est un nombre premier, et k un entier quelconque, alors k^p - k est un multiple de p.

Retour en haut de la page

Ecart entre les nombres premiers :

Il n'existe aucun nombre premier entre n! + 2 et n! + n

En effet :

n! + 2 est multiple de 2 (il n'est donc pas premier)
n! + 3 est multiple de 3
n! + 4 est multiple de 4
n! + 5 est multiple de 5

etc ...

n! + n est multiple de n

Cela signifie qu'en prenant n suffisamment grand, on pourra toujours trouver dans l'ensemble des entier naturel, une suite de nombres consécutifs d'une longueur quelconque ne contenant aucun nombre premier.

Cette remarque suffit à elle seule pour se rendre compte de la raréfaction des nombres premiers : plus on avance dans les entiers naturels en allant vers les "grands nombres", moins il y a de nombres premiers (la densité des nombres premiers diminue). Exemple : entre 0 et 100 il existe 25 nombres premiers, ce qui signifie qu'entre 0 et 100 un nombre entier sur quatre est un nombre premier. Mais ce rapport de 1 nombre premier pour 4 nombre entier diminue rapidement pour les entiers supérieurs à 100 :

Entre 0 et 100 il existe 25 nombres premiers : 25 % des entiers < 100 sont premiers

Entre 0 et 1 000 il existe 168 nombres premiers : 16,8 % des entiers < 1 000 sont premiers

Entre 0 et 1 000 000 il existe 78 498 nombres premiers : 7,84 % des entiers < 1 000 000 sont premiers

Entre 0 et 1 000 000 000 il existe 50 847 534 nombres premiers : 5,08 % des entiers < 1 000 000 000 sont premiers

Faut-il en conclure qu'à partir d'une certaine limite il n'existe plus de nombres premiers ? Non justement, car comme je l'ai déjà démontré en haut de cette page, il existe une infinité de nombres premiers : quelque soit le nombre entier n, il existera toujours un nombre premier supérieur à n.

Retour en haut de la page

Les nombres premiers jumeaux :

Comme nous venons de le voir, entre les nombres n! + 2 et n! + n, aucun nombre n'est premier. En allant assez loin, l'écart entre deux nombres premiers consécutifs est donc aussi grand que l'on veut. Toutefois, cet écart semble aussi égal à 2 une infinité de fois : c'est la conjecture des nombres premiers jumeaux. Par conséquent, l'écart entre nombres premiers consécutifs oscille largement. Sur ces questions, on dispose de nombreuses conjectures vérifiées numériquement, mais de très peu de résultats démontrés. Les mathématiques ressemblent ici à une science expérimentale comme je l'aime : on explore le monde des nombres en tentant d'y repérer des lois, on réussit parfois à lier ces lois entre elles et à les déduire les unes des autres, mais la démonstration des lois elles-mêmes semble impossible avec les moyens actuels.

Parfois, l'écart entre deux nombres premiers consécutifs est égal à 2. C'est le cas pour les couples 3-5, 5-7, 11-13, 17-19 et 29-31 par exemple. De tels nombres premiers sont qualifiés de nombres premiers jumeaux. La date de la première mention des nombres premiers jumeaux est incertaine, mais, depuis un siècle, ils suscitent une grande attention. Leur étude a donné lieu à de nombreuses spéculations mathématiques et à de non moins nombreux calculs informatiques. L'un d'eux, dont les conclusions viennent d'être communiquées, a fait trembler sur sa base la puissante industrie des microprocesseurs. C'est en effet lors du calcul de nombres premiers jumeaux que les bugs sur les premiers microprocesseurs Pentium d'Intel ont été découverts.

D'autres calculs ont révélé de nouvelles propriétés des nombres premiers ; ils prouvent que l'arithmétique ressemble parfois davantage à une discipline expérimentale, telle la physique, qu'à une branche des mathématiques.

Applet Java permettant de trouver une paire de jumeaux

L'applet Java suivante vous permet de connaître la prochaine paire de nombres premiers jumeaux, présentes après un nombre entier donné. Pour l'utiliser, saisissez un nombre entier à 7 chiffres maximum, et appuyez sur le bouton "Rechercher jumeaux". La première paire de jumeaux existante après votre nombre sera alors affichée :

Trouve-t-on toujours des jumeaux ?

Quand on s'intéresse aux nombres premiers jumeaux, la première question qui vient à l'esprit est celle de leur quantité : y en a-t-il une infinité ? Les mathématiciens pensent que oui. Cette affirmation est aujourd'hui l'une des plus célèbres conjectures mathématiques, car tous les efforts pour la démontrer ont été vains : on ne sait ni prouver qu'il existe un nombre infini de nombres premiers jumeaux, ni prouver le contraire. La situation est choquante, car une phrase suffit pour démontrer qu'il existe une infinité de nombres premiers. Les deux problèmes sont très proches, mais l'un est facile, et l'autre bloqué.

Bien sûr, on a effectué des calculs pour s'assurer qu'on trouve toujours des nombres premiers jumeaux, aussi loin qu'on est capable d'aller aujourd'hui. On a tout d'abord compté le nombre précis de premiers jumeaux inférieurs à une borne n. Cette recherche exhaustive a été menée jusqu'à n = 10^15 (un million de milliards) : parmi les 29 844 570 422 669 nombres premiers inférieurs à 10^15, on a compté 1177 209 242 304 paires de nombres premiers jumeaux, soit 3,94 pour cent, et l'on n'a pas constaté que leur suite s'interrompait à une borne quelconque. On a également effectué des sondages bien au-delà de 10^15, sans jamais trouver pour l'instant de zone sans nombres premiers jumeaux.
La plus grande paire de nombres premiers jumeaux connue aujourd'hui est la suivante :

361 700 055 x 2^39 020 - 1 et 361 700 055 x 2^39 020 +1

Chacun de ces nombres s'écrit avec 11 755 chiffres. Cette paire a été "capturée" en 1999 par Henri Lifchitz, un ingénieur électronicien français (c'est important de le signaler), passionné de nombres premiers. Le record immédiatement inférieur, qui date de l'année précédente, est une paire de nombres ayant chacun 11 751 chiffres :

835 335 x 2^39 014 - 1 et 835 335 x 2^39 014 + 1

Ses découvreurs sont Ray Ballinger (chef du service de radiologie du Centre médical de Gainesville, en Floride) et Yves Gallot (ingénieur à Toulouse dans une société spécialisée dans les simulateurs).

Raréfaction chez les raréfiés

On sait que les nombres premiers se raréfient (voir le paragraphe précédent, Ecart entre les nombres premiers) et l'on constate que les nombres premiers jumeaux, considérés dans la suite des nombres premiers, se raréfient également. Un raisonnement heuristique (c'est-à-dire qui suggère sans prouver rigoureusement) conduit à penser que les nombres premiers jumeaux ont une densité de 1/ln(n) parmi les nombres premiers (ou, ce qui revient au même, une densité de 1/ln^2(n) parmi les nombres entiers).

Le raisonnement est simple :
"La probabilité que p et p + 2 soient simultanément premiers est le produit de la probabilité que p soit premier par celle que p + 2 le soit également, car on considère que ces deux événements sont indépendants. Comme le théorème des nombres premiers indique que la probabilité d'être premier tend vers 1/ln(p), la probabilité recherchée tend vers 1/ln(p) x 1/ln(p + 2), soit environ 1/ln^2(p)."

Cet argument est en fait trop peu rigoureux pour constituer une preuve : comme les nombres premiers sont parfaitement déterminés dans la suite des entiers, il est abusif de leur attribuer une probabilité d'occurrence, et plus encore d'en faire des événements indépendants. En outre, le raisonnement est extrêmement dangereux : si on l'applique à p et p + 1, on trouve que la densité des paires de nombres consécutifs qui sont premiers vaut également 1/ln^2(n), alors qu'en réalité, elle est nulle, puisque, quel que soit p, l'un des deux nombres p ou p + 1 est pair ! !

Les nombres premiers jumeaux jusqu'à 2000

Les nombres premiers consécutifs séparés de deux unités (indiqués en rouge dans le tableaux ci-dessous) sont qualifiés de jumeaux. La conjecture des nombres premiers jumeaux affirme qu'il y en a une infinité. Bien qu'on ne sache pas la démontrer, on a formulé la conjecture plus précise (et plus difficile) que leur nombre tend environ vers 1,32 n/ln^2(n) parmi les nombres inférieurs à n.

2	3	5	7	11	13	17	19	23	29
31	37	41	43	47	53	59	61	67	71
73	79	83	89	97	101	103	107	109	113
127	131	137	139	149	151	157	163	167	173
179	181	191	193	197	199	211	223	227	229
233	239	241	251	257	263	269	271	277	281
283	293	307	311	313	317	331	337	347	349
353	359	367	373	379	383	389	397	401	409
419	421	431	433	439	443	449	457	461	463
467	479	487	491	499	503	509	521	523	541
547	557	563	569	571	577	587	593	599	601
607	613	617	619	631	641	643	647	653	659
661	673	677	683	691	701	709	719	727	733
739	743	751	757	761	769	773	787	797	809
811	821	823	827	829	839	853	857	859	863
877	881	883	887	907	911	919	929	937	941
947	953	967	971	977	983	991	997	1009	1013
1019	1021	1031	1033	1039	1049	1051	1061	1063	1069
1087	1091	1093	1097	1103	1109	1117	1123	1129	1151
1153	1163	1171	1181	1187	1193	1201	1213	1217	1223
1229	1231	1237	1249	1259	1277	1279	1283	1289	1291
1301	1303	1307	1319	1321	1327	1361	1367	1373	1381
1399	1409	1423	1427	1429	1433	1439	1447	1451	1453
1459	1471	1481	1483	1487	1489	1493	1499	1511	1523
1531	1543	1549	1553	1559	1567	1571	1579	1583	1597
1601	1607	1609	1613	1619	1621	1627	1637	1657	1663
1667	1669	1693	1697	1699	1709	1721	1723	1733	1741
1747	1753	1759	1777	1783	1787	1789	1801	1811	1823
1831	1847	1861	1867	1871	1873	1877	1879	1889	1901
1907	1913	1931	1933	1949	1951	1973	1979	1987	1993
1997	1999	2003	2011	2017	2027	2029	2039	2053	etc.

On constate dans ce tableau qu'il existe exactement 60 paires
de nombres premiers jumeaux entre 0 et 2000

Remarque : le seul entier appartenant à 2 paires de jumeaux est le 5. En effet, 5 appartient à la fois la paire de jumeaux (3;5) et à la paire (5;7). Aucun autre entier peut appartenir à 2 paires de nombres premiers jumeaux, puisque si on considère les 3 entiers impairs consécutifs p, p+2, et p+4 (avec p>3 et p impair), il y en aura forcément un des 3 qui est multiple de 3. Les 3 nombres entiers impairs consécutifs étant tous les 3 premiers sont donc seulement 3, 5, et 7.

La fonction 2 (m)

Nous avons vu que la fonction (m) représentait le nombre de nombres premiers inférieurs ou égaux à m. De la même manière, on définie la fonction 2 (m) qui est égale, quelque soit le réel m, au nombre de nombres premiers jumeaux inférieurs ou égaux à m. Par exemple, nous venons de voir qu'il existe exactement 60 paires de nombres premiers jumeaux entre 0 et 2000, on peut donc écrire 2 (2000)=119 (et pas 120, car le nombre 5, compté une seule fois, est présent dans 2 paires de jumeaux).

Raréfaction des nombres premiers jumeaux

n	nombre de nombres premiers < n	nombre de paires de nombres premiers jumeaux < n	pourcentage parmi les premiers
10^3	168	35	20,83
10^4	1 229	205	16,68
10^5	9 592	1 224	12,76
10^6	78 498	8 169	10,41
10^7	664 579	58 980	8,87
10^8	5 761 455	440 312	7,65
10^9	50 847 534	3 424 506	6,73
10^10	455 052 511	27 412 679	6,02
10^11	4 118 054 813	224 376 048	5,45
10^12	37 607 912 018	1 870 585 220	4,97
10^13	346 065 536 839	15 834 664 872	4,56
10^14	3 204 941750 802	135 780 321665	4,22
10^15	29 844 570 422 669	1 177 209 242 304	3,94

Les plus grandes paires de nombres premiers jumeaux connues

Premiers jumeaux	Nombre de chiffres	Découvreur	Année
361 700 055 x 2 ^ 39 020 ± 1	11 755	Lifchitz	1999
835 335 x 2 ^ 39 014 ± 1	11 751	Ballinger et Gallot	1998
242 206 083 x 2 ^ 38 880 ± 1	11 713	Jarai et Indlekofer	1995
40 883 037 x 2 ^ 23 456 ± 1	7 069	Lifchitz et Gallot	1998

Des débuts de preuves ?

Voici une façon indirecte de formuler la conjecture des nombres premiers jumeaux, en mettant leur écart en avant :

Le nombre 2 peut s'écrire d'une infinité de façons différentes sous la forme p1 -p2, où p1 et p2 sont des nombres premiers.
En utilisant la technique des cribles (généralisation de l'idée du crible d'Ératosthène), on a démontré des résultats qui approchent cet énoncé et qui sont loin d'être anecdotiques. En 1920, le mathématicien norvégien Viggo Brun a ainsi prouvé que :

Le nombre 2 peut s'écrire d'une infinité de façons différentes sous la forme p1 -p2, où p1 et p2 sont des nombres "9-presque-premiers".

Un nombre "k-presque-premier" est un nombre dont la décomposition en facteurs premiers possède k facteurs au plus. Le nombre 12 = 2 x 2 x 3 est 3-presque-premier ; le nombre 169 = 13 x 13 est 2-presque-premier.

Le résultat de Brun sur l'infinité des nombres 9-presque-premiers jumeaux, s'il tend une passerelle vers la conjecture des nombres premiers jumeaux, est encore très loin du but : celui-ci sera atteint quand on aura remplacé "9-presque-premiers" par "1-presque-premiers", puisque "être 1-presque-premier" équivaut bien sûr à "être premier".

Toutefois, les progrès ont été continus. En 1924, H. Rademacher a remplacé le "9" par "7", et, à la suite de travaux de A. Rényi en 1947 et de J. Chen en 1966, on sait aujourd'hui que :

Le nombre 2 peut s'écrire d'une infinité de façons différentes sous la forme p1-p2, avec p1 premier et p2 un nombre 2-presque-premier.

Un dernier effort : il n'y a plus qu'à remplacer 2-presque-premier par 1-presque-premier !

La constante de Brun

On observe que les nombres premiers jumeaux se raréfient parmi les nombres premiers. Peut-on le prouver ? Il existe un moyen d'évaluer la taille d'un ensemble infini : la série des inverses de ses éléments. On ignore bien sûr si les nombres premiers jumeaux sont en nombre infini, mais on peut savoir, au moyen de cette série des inverses, s'ils sont infiniment moins nombreux que les nombres premiers.

En 1919, Brun prouva que la série des inverses des nombres premiers jumeaux était convergente. Autrement dit, la série

possède une valeur finie, contrairement à la série des inverses des nombres premiers, dont on a prouvé qu'elle est infinie :

Remarquez que, dans la série des inverses des nombres premiers jumeaux, on fait apparaître deux fois 1/5, car c'est le second élément de la paire (3;5), en même temps que le premier élément de la paire (5;7).

La valeur finie de cette série indique qu'il y a infiniment moins de nombres premiers jumeaux que de nombres premiers. Le raisonnement suivant le fera mieux comprendre : si, en moyenne, un nombre premier sur 100 était un nombre premier jumeau, alors la série des inverses des nombres premiers jumeaux se comporterait comme celle des inverses des nombres premiers et serait infinie (car l'infini divisé par 100 est encore l'infini). Il en résulte que moins d'un nombre premier sur 100 est un nombre premier jumeau. Ce qui vient d'être dit pour 100 peut être répété avec 1000, 10 000, etc. Il y a bien raréfaction : en allant assez loin, la proportion des nombres premiers jumeaux tend vers 0.
Le même Brun a d'ailleurs démontré un résultat précis de majoration : le nombre 2 (m) de nombres premiers jumeaux inférieurs ou égaux à m est inférieur à 100m/ln^2(m), quantité qui devient négligeable par rapport à (m), le nombre de nombres premiers inférieurs ou égaux à m, quand m tend vers l'infini.

D'après tout ce qui précède, on conclut qu'il existe des séquences de plus en plus longues de nombres premiers consécutifs qui ne comportent aucun couple de nombres premiers jumeaux : plus on va loin, moins l'écart de 2 est fréquent. Ce résultat complète ce que l'on savait déjà de l'écart entre les nombres premiers : il existe des séquences de nombres composés successifs aussi longues que l'on veut, car tous les nombres entre n! + 2 et n! + n sont composés (n! + 2 est un multiple de 2 ; n! + 3 est un multiple de 3 ; ... ; n! + n est un multiple de n).

Revenons à la convergence de la série des inverses des nombres premiers jumeaux. On doit souligner que ce résultat, s'il prouve que les jumeaux se raréfient parmi les premiers, ne résout pas la question de savoir s'il existe ou non une infinité de nombres premiers jumeaux : la série peut avoir une valeur finie parce que ses termes sont en nombre fini, ou parce qu'ils sont de plus en plus rares, bien qu'en nombre infini.

Cette valeur finie de la série, nommée constante de Brun et notée B en l'honneur de celui qui a prouvé la convergence, est estimée à :

On ne sait presque rien de cette constante, pas même si c'est un nombre rationnel (pouvant être écrit sous la forme d'une fraction) ou irrationnel (comme racine carrée de 2), algébrique (solution d'une équation polynomiale à coefficients entiers, comme racine cubique de 2 solution de x^3 = 2) ou transcendant (non algébrique, comme Pi). Elle est particulièrement difficile à évaluer, et l'on ne sait pas la calculer autrement qu'en utilisant directement sa définition (à l'exception toutefois d'une petite astuce d'extrapolation sur le résultat brut). Pour connaître B, il faut donc aller très loin dans la série des nombres premiers.

Valeur de la constante de Brun constatée expérimentalement avec Mathematica :

En utilisant tous les jumeaux compris entre le 1 er le 1 000 000 ème nombre premier : B = 1,74268

Quelques propriétés des nombres premiers jumeaux

n est le premier élément d'une paire de nombres premiers jumeaux si, et seulement si 4((n -1)! + 1) + n est un multiple de n(n + 2)

(ou (n -1)!-( 3n + 2) + 2n + 2 est un multiple de n(n + 2) )
(ou (n -1)! (n - 2) - 2 est un multiple de n(n + 2) )

De la première condition, on déduit la formule suivante, qui engendre tous les premiers éléments des paires de nombres premiers jumeaux quand n décrit l'ensemble des entiers naturels :

j(n) = 3+n [(4(n+2)!+n+7)/(n+3)(n+5) - [(4(n + 2)! + n + 6)/(n + 3)(n + 5)]]

La formule fonctionne de la façon suivante : à n, on fait correspondre n + 3 ; pour n = 0, on obtient ainsi 3, le premier nombre premier jumeau. La première des trois conditions de gémellité énoncées plus haut devient alors : n + 3 est le premier élément d'une paire de jumeaux si, et seulement si, 4(n + 2)! + n + 7 est un multiple de (n + 3)(n + 5). Dans ce cas, le rapport de ces deux expressions est un entier, et la partie entière (symbolisée par les crochets dans l'expression ci-dessus) de (4(n + 2)! + n + 6) / (n + 3)(n + 5) est l'entier immédiatement inférieur. La partie entière de leur différence vaut alors 1, et 0 sinon. Par conséquent, j(n) = 3 + n si 3 + n est le premier élément d'une paire de jumeaux, et j(n) = 3 dans les autres cas.

Un polynôme qui donne tous les nombres premiers jumeaux

Le polynôme ci-dessous est dû à Christoph Baxa, du département de mathématiques de l'Université de Vienne, qui l'a tiré de la théorie des équations diophantiennes. Quand les variables a, b,..., z décrivent l'ensemble des entiers naturels, les valeurs positives du polynôme décrivent l'ensemble des nombres p tels que (p, p + 2) est une paire de nombres premiers jumeaux. L'avantage de cette formule sur celle du paragraphe précédent est qu'elle ne fait pas appel à la fonction partie entière :

(k+2) [1-(wz+h+j-q)^2-((g+1)(h+j)+h-z)^2
- (p + q + z + 2n - e)^2 - (e^3 (e + 2)(a + 1)^2 + 1- o^2)^2
- ((a^2 -1)(n + l + v)^2 + 1-x^2)^2 - (16(a^2 -1)(n + l + v)^2 + 1-x^2)^2
- (((a + u^2(u^2 - a)^2 -1)(n + 4d(n + l + v))^2 + 1- (x + cu)^2)^2
-((a^2-1)l^2 + 1-m^2)^2 -(p + l(a -n -1) + b(2a(n + 1)-(n + 1)^2-1) -m)^2
-(q+(n+l+v)(a-p-1)+s(2a(p+1)-(p+1)^2-1)-x)^2
- (z + pl(a -p) + t(2ap -p^2 -1) -pm)^2
- (16(k + 1)^3(k + 2)(n + 1)^2 + 1- f^2)^2
- (k + 1 + ia - i - l)^2 - (4g + k + 10 -y(k + 2)(k + 4))^2]

Rappel : l'opérateur ^ symbolise ici la fonction puissance, prioritaire sur la multiplication.

Retour en haut de la page

Les nombres premiers triplets et quadruplets :

Après nous être intéressé à l'écart entre deux nombres premiers consécutifs, élargissons la question à la suite des écarts de trois, puis quatre nombres premiers consécutifs.

Les nombres premiers triplets

Commençons par les suites de trois nombres premiers consécutifs. A l'exception de 3, 5, 7, trois nombres premiers consécutifs ne peuvent pas être de la forme p, p+2, p+4. En effet, dans toute série de cette forme, l'un au moins des trois nombres est multiple de 3.

On trouve en revanche que p, p+2, p+6 et p, p+4, p+6 sont des formes possibles pour trois nombres premiers consécutifs. On appelle nombres premiers triplets, l'ensemble de trois nombres premiers consécutifs, de la forme p, p+2, p+6 ou de la forme p, p+4, p+6. Il existe donc 2 formes de nombres premiers triplets.

Remarque : pour les nombres premiers jumeaux, il n'existait qu'une seule forme, qui est p, p+2.

Applet Java permettant de trouver des nombres premiers triplets

L'applet Java suivante permet de rechercher des nombres premiers triplets. Vous devez préciser la forme de triplets à rechercher, ainsi que le nombre à partir duquel débutera la recherche :

Les nombres premiers quadruplets

Quand on considère des suites de quatre nombres premiers consécutifs, on s'aperçoit que la seule forme possible ayant pour extrémités p et p+8 (cet écart de 8 entre les deux extrémités étant le plus petit possible) est p, p+2, p+6, p+8. On appelle nombres premiers quadruplets, l'ensemble de quatre nombres premiers consécutifs de la forme p, p+2, p+6, p+8.

Applet Java permettant de trouver des nombres premiers quadruplets

L'applet Java suivante permet de rechercher des nombres premiers quadruplets. Vous devez simplement préciser le nombre à partir duquel débutera la recherche :

Retour en haut de la page