Les unités de mesure utilisées en Sciences de l'Ingénieur

Cet article récapitule plus de 20 unités de mesure à connaître en première et terminale S, dans le but d'en clarifier leurs liens, leurs définitions, et leur décomposition dans le système international d'unités de mesure (kg m A s).

Les unités de mesure et les grandeurs physiques sont chacune symbolisées par une lettre. Afin de limiter les ambiguïtés, bien que le contexte d'application distingue les unités des grandeurs, deux couleurs différentes sont utilisées ici :

• les unités de mesure sont écrites en rouge
• les grandeurs physiques sont écrites en vert

Exemple : m représente un mètre (c'est une unité de mesure car elle est en rouge) alors que m représente la masse (c'est une grandeur physique car elle est en vert).

Sommaire de cette page Liste des 22 unités de mesure Les 10 relations fondamentales de mécanique Les 10 relations fondamentales d'électronique Décomposition des unités dans le système international Comment retenir tout ça ? Pour aller plus loin Grandeur d'effort et grandeur de flux Conversion de certaines unités Décomposition de 36 unités de mesure dans le système international Les autres unités de mesure utilisées en physique-chimie Liste des physiciens qui ont donné leur nom aux unités

 

Retour au sommaire

 

Les 22 unités de mesure utilisées en sciences de l'ingénieur sont ici classées en 3 catégories :

• 6 unités élémentaires utilisées dans toutes les matières scientifiques
• 8 unités utilisées surtout en mécanique
• 8 unités utilisées surtout en électronique

Les 6 unités élémentaires
Nom de l'unité de mesure	Symbole de l'unité de mesure	Nom de la grandeur physique mesurée	Symbole de la grandeur physique
seconde kilogramme	s kg	temps masse	t m
mètre mètre carré	m m2	longueur surface	l S
watt joule	W J	puissance énergie	P W

Remarque : dans le système international l'unité de mesure de la masse est le kilogramme et non le gramme.

 

Les 8 unités de mécanique
Nom de l'unité de mesure	Symbole de l'unité de mesure	Nom de la grandeur physique mesurée	Symbole de la grandeur physique
newton pascal	N Pa	force pression	F p
mètre par seconde radian par seconde	m.s-1 rad.s-1	vitesse linéaire vitesse angulaire	v Ω
newton mètre mètre par seconde carrée	N.m m.s-2	couple (ou moment d'une force) accélération	c a
kilogramme mètre par seconde kilogramme mètre carré	kg.m.s-1 kg.m2	quantité de mouvement moment d'inertie	q J

Remarque : les unités de mesure mécaniques obsolètes ou hors système international sont à proscrire de nos jours. C'est le cas par exemple du Bar pour la pression (la pression se mesure en Pascal dans le système international, on ne parle donc plus de Bar depuis longtemps), ou du tour par seconde pour la vitesse de rotation (l'unité internationale du scientifique est le radian par seconde). De même, le "travail" n'est pas une grandeur physique : il faut parler d'énergie mesurée en Joule ou en Newton mètre. Un dernier exemple : la puissance mécanique d'un moteur ne se mesure plus en chevaux depuis plusieurs décennies (en fait depuis que la diligence a disparu ...) : elle se mesure exclusivement en watt aujourd'hui !

 

Les 8 unités d'électronique
Nom de l'unité de mesure	Symbole de l'unité de mesure	Nom de la grandeur physique mesurée	Symbole de la grandeur physique
volt ampère	V A	tension courant	U I
ohm siemens	Ω S	résistance conductance	R G
farad henry	F H	capacité inductance	C L
coulomb weber	C Wb	quantité d'électricité flux magnétique	Q Φ

Remarque : la conductance G mesurée en siemens est l'inverse de la résistance R mesurée en ohm : G=1/R

On peut en déduire que 1 S = 1 Ω^-1 (un siemens est l'inverse d'un ohm)

Pour réviser toutes ces unités de mesure dans un QCM cliquez ici (choisissez le thème "Les unités de mesure : NIVEAU 1").

 

Retour au sommaire

 

Avant d'énoncer les 20 relations fondamentales à connaître, rappelons la définition de 4 unités de mesure.

Définition du newton : Force qui communique, à un corps ayant une masse de 1 kilogramme, une accélération de 1 mètre par seconde carrée. Définition du pascal : Pression uniforme qui, agissant sur une surface plane de 1 mètre carré, exerce perpendiculairement à cette surface une force totale de 1 newton. Définition du joule : Energie produite par une force de 1 newton dont le point d'application se déplace de 1 mètre dans la direction de la force. Définition du watt : Puissance d'un système énergétique dans lequel est transférée uniformément une énergie de 1 joule pendant 1 seconde.

Relation produit entre les unités de mesure

Le tableau suivant décrit les 10 relations fondamentales concernant les grandeurs physiques utilisées surtout en mécanique. A partir de chacune de ces relations entre grandeurs physiques (relations appelées familièrement "des formules") nous dégagerons systèmatiquement une relation produit entre les unités de mesure.

Une relation produit est de la forme A = B x C, où A B et C sont 3 unités de mesure distinctes, mais liées. La relation produit A = B x C peut bien sûr s'écrire de 3 manières différentes mais équivalentes : A = B x C <=> B = A / C <=> C = A / B (1 relation produit et 2 relations quotient). De ces 3 écritures strictement équivalentes nous ne garderons que la relation produit A = B x C (à convertir ultérieurement en relation quotient en cas de besoin).

Remarque : en mécanique l'énergie (en Joule) est parfois appelée "travail", la force (en Newton) est parfois appelée "effort", la pression (en Pascal) est parfois appelée "contrainte", et le couple (en Newton Mètre) est parfois appelé "moment".

Les 10 relations fondamentales de mécanique
N°	Désignation	Relation entre les grandeurs	Relation entre les grandeurs physiques en toutes lettres	Relation produit entre les unités
1	Force d'un système statique	F=p.S	force = pression x surface	1 N = 1 Pa x 1 m2
2	Force d'un système dynamique	F=m.a	force = masse x accélération	1 N = 1 kg x 1 m.s-2
3	Puissance d'un système mécanique de rotation	P=c.Ω	puissance = couple x vitesse angulaire	1 W = 1 N.m x 1 rad.s-1
4	Puissance d'un système mécanique de translation	P=F.v	puissance = force x vitesse linéaire	1 W = 1 N x 1 m.s-1
5	Energie développée par un système de puissance P pendant un temps t	W=P.t	énergie = puissance x temps	1 J = 1 W x 1 s
6	Energie développée par une force F produisant un déplacement d	W=F.d	énergie = force x distance	1 J = 1 N x 1 m
7	Quantité de mouvement d'une masse m se déplaçant à la vitesse v	q=m.v	quantité de mouvement = masse x vitesse linéaire	1 kg.m.s-1 = 1 N.s
8	Energie potentielle de pesanteur d'une masse m à une altitude z	W=m.g.z	énergie = masse x accélération x altitude	1 J = 1 kg x 1 m.s-2 x 1 m
9	Energie dans un système mécanique de rotation	W=(J.Ω2)/2	énergie = ½ x moment d'inertie x vitesse angulaire ²	1 J = 1 kg x 1 m2.s-2
10	Energie dans un système mécanique de translation	W=(m.v2)/2	énergie = ½ x masse x vitesse linéaire²	1 J = 1 kg x 1 m2.s-2

 

Remarques et commentaires :

• dans les relations 2, 7 et 10 la masse m est en kilogramme (et non en gramme)
• la relation 1 nous montre que 1 pascal est égal à 1 newton divisé par 1 mètre carré (1 Pa = 1 N / 1 m² = 1 N x 1 m^-2) : 1 Pa = 1 N.m^-2
• la relation 5 n'est pas propre à un système mécanique et reste valable quelque soit le type d'énergie (électrique, mécanique, ou autre)
• la relation 5 nous rappelle que la réunion d'un watt avec 1 seconde (1 watt pendant un temps d'une seconde) développe une énergie d'un joule, ce qui signifie qu'un joule est strictement équivalent à un watt seconde : 1 J = 1 W.s
• les relations 2 et 10 nous montrent que 1 J = 1 N.m = 1 N x 1 m. En effet la relation 2 nous dit que 1 N = 1 kg x 1 m.s^-2, et en multipliant par 1 mètre on obtient 1 N.m = 1 kg x 1 m².s^-2. Or la relation 6 nous dit que 1 kg x 1 m².s^-2 correspond à 1 joule.
• la relation 6 nous rappelle directement que 1 J = 1 N.m
• les relations 3 et 4 nous donnent deux définitions de la puissance mécanique. La différence entre les deux est que dans la relation 3 le mètre est "accroché" au newton (dans le couple) alors que dans la relation 4 le mètre est "accroché" à la vitesse. Dans les deux cas on en déduit que 1 W = 1 N.m.s^-1
• en multipliant les deux membres de la relation produit entre les unités n°3 par une seconde, et sachant que le radian n'est pas une unité de mesure, on retrouve la relation 1 W.s = 1 N.m
• de même, en multipliant les deux membres de la relation produit entre les unités n°4 par une seconde on retrouve à nouveau la relation 1 W.s = 1 N.m
• la relation 7 nous donne un exemple d'unité composée (le "kilogramme mètre par seconde" : 1 kg.m.s^-1 = 1 kg x 1 m.s^-1) qui ne possède pas de nom ou de "raccourcis" simple (contrairement par exemple au "kilogramme mètre carré par seconde carrée" qui s'appelle un Joule). Cette relation 6 nous dit surtout qu'un solide de masse m élancé à la vitesse linéaire v est chargé d'une quantité de mouvement égale au produit de la masse par la vitesse
• contrairement à la force qui s'annule à vitesse constante (voir la relation 2 donnant le principe fondamental de la dynamique), la quantité de mouvement existe à partir du moment ou la vitesse du solide est non nulle (même à accélération nulle)
• mais sachant que 1 N = 1 kg x 1 m.s^-2 (voir la relation 2) on peut remarquer que le "kilogramme mètre par seconde" n'est autre qu'un newton multiplié par une seconde. On en déduit que la quantité de mouvement se mesure en newton seconde : 1 kg.m.s^-1 = 1 N.s
• en comparant les relations 2 et 7 et leurs unités on peut donc remarquer d'un kilogramme mètre par seconde est équivalent à un newton seconde : 1 kg.m.s^-1 = 1 kg.m.s^-2 x 1 s = 1 N x 1 s = 1 N.s = 1 "newton seconde"
• pour la relation 2, si l'accélération considérée est l'accélération de la pesanteur g, alors la force obtenue correspond au poids : p=m.g
• la relation 5 nous rappelle que la puissance est la dérivée de l'énergie par rapport au temps (multiplication par t = dérivée par rapport à t, et division par t = intégration par rapport à t)
• sachant que l'accélération est la dérivée de la vitesse, les relations 2 et 7 nous disent que la force est la dérivée de la quantité de mouvement : en dérivant la relation 7 par rapport au temps on obtient la relation 2 (m étant constante)

 

Récapitulatif des nouvelles relations suite aux remarques précédentes

Concernant les unités de mesure il faut retenir que :

1 N.m = 1 J = 1 W.s	énergie
1 N.m-2 = 1 Pa	pression
1 N.kg-1 = 1 m.s-2	accélération
1 N.s = 1 kg.m.s-1	quantité de mouvement

 

Concernant les grandeurs physiques, on retient qu'il y a deux manières d'exprimer la puissance mécanique :

puissance = couple x vitesse angulaire = force x vitesse linéaire

Ce qui nous conduit à deux définitions de l'énergie mécanique (en multipliant la relation précédente par le temps) :

énergie = couple = force x longueur

Ce qui nous rappelle une fois de plus que le joule est équivalent au newton mètre : 1 J = 1 N.m

 

Et la notion de quantité de mouvement nous a permis de remarquer que 1 kg.m.s^-1 = 1 N.s, soit :

masse x vitesse linéaire = force x temps

Ce qui revient au principe fondamental de la dynamique (en divisant la relation précédente par le temps) :

masse x accélération = force

Ce qui nous ramène au point de départ, à savoir la définition du Newton : 1kg.m.s^-2 = 1 N

Enfin on déduira également que l'accélération est le rapport entre la force et la masse : 1 m.s^-2 = 1 N.kg^-1

Application : l'accélération de la pesanteur g peut aussi bien s'exprimée en mètre par seconde carrée qu'en newton par kilogramme : g = 9.81 m.s^-2 = 9.81 N.kg^-1

La boucle est bouclée et tout ceci est donc parfaitement cohérent.

 

Retour au sommaire

 

Les 10 relations fondamentales d'électronique

Le tableau suivant décrit les 10 relations fondamentales concernant les grandeurs physiques utilisées surtout en électronique. Comme la plupart des unités de mesure sont utilisées plusieurs fois dans ce tableau nous allons pouvoir dégager de ce tableau plusieurs définitions pour chacune des unités, en utilisant les relations produit ou en les convertissant en relations quotient.

Les 10 relations fondamentales d'électronique
N°	Désignation	Relation entre les grandeurs	Relation entre les grandeurs physiques en toutes lettres	Relation produit entre les unités
11	Puissance d'un système électrique	P=U.I	puissance = tension x courant	1 W = 1 V x 1 A
12	Tension dans une résistance électrique ("loi d'ohm")	U=R.I	tension = résistance x courant	1 V = 1 Ω x 1 A
13	Quantité d'électricité dans un circuit électrique	Q=I.t	quantité d'électricité = courant x temps	1 C = 1 A x 1 s
14	Quantité d'électricité dans un condensateur	Q=C.U	quantité d'électricité = capacité x tension	1 C = 1 F x 1 V
15	Flux magnétique dans un circuit électrique	Φ=U.t	flux = tension x temps	1 Wb = 1 V x 1 s
16	Flux magnétique dans une bobine	Φ=L.I	flux = inductance x courant	1 Wb = 1 H x 1 A
17	Constante de temps d'un circuit RC	t=R.C	temps = résistance x capacité	1 s = 1 Ω x 1 F
18	Constante de temps d'un circuit RL	t=L/R	temps = inductance / résistance	1 H = 1 Ω x 1 s
19	Energie emmagasinée dans un condensateur	W=(C.U2)/2	énergie = ½ x capacité x tension²	1 J = 1 F x 1 V²
20	Energie emmagasinée dans une bobine	W=(L.I2)/2	énergie = ½ x inductance x courant²	1 J = 1 H x 1 A²

Remarques et commentaires :

• la relation 11 nous dit que 1 watt = 1 volt ampère. Or nous savons déjà que 1 watt = 1 joule par seconde :

  ⇒ 1 watt = 1 volt ampère = 1 volt x 1 ampère

  ⇒ 1 watt = 1 joule par seconde = 1 joule / 1 seconde

• l'ohm est utilisé dans 3 relations. Nous pouvons donc écrire 3 définitions d'un ohm :

  ⇒ d'après la relation 12 : 1 ohm = 1 volt par ampère = 1 volt / 1 ampère

  ⇒ d'après la relation 17 : 1 ohm = 1 seconde par farad = 1 seconde / 1 farad

  ⇒ d'après la relation 18 : 1 ohm = 1 henry par seconde = 1 henry / 1 seconde

• le volt est utilisé dans 4 relations. Nous pouvons donc écrire 4 définitions d'un volt :

  ⇒ d'après la relation 11 : 1 volt = 1 watt par ampère = 1 watt / 1 ampère

  ⇒ d'après la relation 12 : 1 volt = 1 ohm ampère = 1 ohm x 1 ampère

  ⇒ d'après la relation 14 : 1 volt = 1 coulomb par farad = 1 coulomb / 1 farad

  ⇒ d'après la relation 15 : 1 volt = 1 weber par seconde = 1 weber / 1 seconde

• l'ampère est utilisé dans 4 relations. Nous pouvons donc écrire 4 définitions d'un ampère :

  ⇒ d'après la relation 11 : 1 ampère = 1 watt par volt = 1 watt / 1 volt

  ⇒ d'après la relation 12 : 1 ampère = 1 volt par ohm = 1 volt / 1 ohm

  ⇒ d'après la relation 13 : 1 ampère = 1 coulomb par seconde = 1 coulomb / 1 seconde

  ⇒ d'après la relation 16 : 1 ampère = 1 weber par henry = 1 weber / 1 henry

• le coulomb est utilisé dans 2 relations. Nous pouvons donc écrire 2 définitions d'un coulomb :

  ⇒ d'après la relation 13 : 1 coulomb = 1 ampère seconde = 1 ampère x 1 seconde

  ⇒ d'après la relation 14 : 1 coulomb = 1 farad volt = 1 farad x 1 volt

• le weber est utilisé dans 2 relations. Nous pouvons donc écrire 2 définitions d'un weber :

  ⇒ d'après la relation 15 : 1 weber = 1 volt seconde = 1 volt x 1 seconde

  ⇒ d'après la relation 16 : 1 weber = 1 henry ampère = 1 henry x 1 ampère

• le farad est utilisé dans 2 relations. Nous pouvons donc écrire 2 définitions d'un farad :

  ⇒ d'après la relation 14 : 1 farad = 1 coulomb par volt = 1 coulomb / 1 volt

  ⇒ d'après la relation 17 : 1 farad = 1 seconde par ohm = 1 seconde / 1 ohm

• le henry est utilisé dans 2 relations. Nous pouvons donc écrire 2 définitions d'un henry :

  ⇒ d'après la relation 16 : 1 henry = 1 weber par ampère = 1 weber / 1 ampère

  ⇒ d'après la relation 18 : 1 henry = 1 ohm seconde = 1 ohm x 1 seconde

 

Les relations 13, 14 et 17 sont équivalentes : si on en connaît deux on en déduit la troisième :

En remplaçant le temps dans la relation 13 par la définition de t donnée dans la relation 17 on obtient la relation 14 :

Q = I.t = I.R.C = U.C puisque R.I=U

Les relations 13 et 14 (donnant deux définitions du coulomb) nous disent qu'un ampère seconde est équivalent à un farad volt :

1 A.s = 1 F.V = 1 C

Cette égalité peut nous donner la définition d'un farad, d'une seconde ou d'un ohm donnée par la relation 17 :

• En divisant 1 A.s = 1 F.V par 1 V on obtient 1 F = 1 s.Ω^-1 (comme l'indique la relation 17)
• En divisant 1 A.s = 1 F.V par 1 A on obtient 1 s = 1 F.Ω (comme l'indique la relation 17)
• En divisant 1 A.s = 1 F.V par 1 F.A on obtient 1 Ω = 1 s.F^-1 (comme l'indique la relation 17)

Conclusion :

• la relation 17 n'est qu'une conséquence des relations 13 et 14 et n'apporte rien de nouveau
• si Q = I.t et Q = C.U alors on en déduit forcément que t = R.C

 

Les relations 15, 16 et 18 sont équivalentes : si on en connaît deux on en déduit la troisième :

En remplaçant le temps dans la relation 15 par la définition de t donnée dans la relation 18 on obtient la relation 16 :

Φ = U.t = U.L/R = L.I puisque U/R=I

Les relations 15 et 16 (donnant deux définitions du weber) nous disent qu'un volt seconde est équivalent à un henry ampère :

1 V.s = 1 H.A = 1 Wb

Cette égalité peut nous donner la définition d'un henry, d'une seconde ou d'un ohm donnée par la relation 18 :

• En divisant 1 V.s = 1 H.A par 1 A on obtient 1 H = 1 s.Ω (comme l'indique la relation 18)
• En divisant 1 V.s = 1 H.A par 1 V on obtient 1 s = 1 H.Ω^-1 (comme l'indique la relation 18)
• En divisant 1 V.s = 1 H.A par 1 A.s on obtient 1 Ω = 1 H.s^-1 (comme l'indique la relation 18)

Conclusion :

• la relation 18 n'est qu'une conséquence des relations 15 et 16 et n'apporte rien de nouveau
• si Φ = U.t et Φ = L.I alors on en déduit forcément que t = L/R

 

Récapitulatif des nouvelles relations entre unités suite aux remarques précédentes :

Unité	Exemples d'expressions en fonction d'autres unités
le WATT	1 W = 1 V.A = 1 J.s-1
l'OHM	1 Ω = 1 V.A-1 = 1 s.F-1 = 1 H.s-1
le VOLT	1 V = 1 W.A-1 = 1 Ω.A = 1 C.F-1 = 1 Wb.s-1
l'AMPERE	1 A = 1 W.V-1 = 1 V.Ω-1 = 1 Wb.H-1 = 1 C.s-1
le COULOMB	1 C = 1 A.s = 1 F.V
le WEBER	1 Wb = 1 V.s = 1 H.A
le FARAD	1 F = 1 s.Ω-1 = 1 C.V-1
le HENRY	1 H = 1 s.Ω = 1 Wb.A-1

Bien que chacune des unités de mesure puisse se définir de différentes manières en fonctions des autres unités, s'il n'y avait qu'une seule relation à retenir pour chacune de ces 8 unités ce serait la suivante :

1 W = 1 J.s-1	1 Ω = 1 V.A-1
1 V = 1 W.A-1	1 A = 1 W.V-1
1 C = 1 A.s	1 Wb = 1 V.s
1 F = 1 s.Ω-1	1 H = 1 Ω.s

Rappel : le siemens est l'inverse (au sens mathématique) d'un ohm : 1 S = 1 Ω^-1. On peut donc remplacer dans les relations ci-dessus 1 Ω^-1 par 1 S et remplacer 1 Ω par 1 S^-1. Exemples de relations obtenues en utilisant le siemens : 1 F = 1 s.S (1 farad = 1 seconde siemens = 1 seconde x 1 siemens), 1 H = 1 s.S^-1 (1 henry = 1 seconde par siemens = 1 seconde / 1 siemens), etc.

Pour vous entraîner et réviser toutes ces relations dans un QCM cliquez ici (choisissez un des 2 thèmes "Les unités de mesure").

 

Retour au sommaire

 

Le Système International d'Unités a pour objet une meilleure uniformité, donc une meilleure compréhension mutuelle dans l'usage général de la mesure. Le Système International d'Unités est un système cohérent d'unités qui comporte des unités de base et des unités dérivées. Les 4 unités de base du système international sont le kilogramme, le mètre, l’ampère et la seconde. Toutes les autres unités habituellement employées sont des unités dérivées résultant de la composition des unités de base.

Nous allons voir ici comment retrouver la décomposition en kg m A et s de chacune des 20 unités de mesures décrites ci-dessus, sans rien apprendre par coeur et en utilisant seulement (et intelligemment) les remarques des paragraphes précédents.

Certaines unités sont faciles à décomposer en kg m A s dès qu'on en a compris la définition (c'est le cas par exemple du Newton ou du Coulomb). Par contre, pour d'autres l'exercice parait moins évident. Par exemple, quel rapport y'a-t-il entre un volt et un kilogramme ? Quel lien existe-t-il entre un ohm et un mètre ? ?

En suivant ce qui suit vous allez tout doucement retrouver sans difficulté la décomposition des 20 unités.

Le point de départ (qui est très important) sera la définition d'un newton : un newton est la force qui communique, à un corps ayant une masse de 1 kilogramme, une accélération de 1 mètre par seconde carrée. En d'autre termes une masse de 1 kg animée d'une accélération de 1 m.s^-2 possède une force de 1 newton (c'est ce que nous a déjà dit la relation n°2). On en déduit que 1 N = 1 kg x 1 m.s^-2 = 1 kg.m.s^-2. Et voilà déjà la décomposition du newton dans le système international kg m A et s.

Question : comment retrouver la décomposition d'un newton ? Solution : il faut utiliser la définition d'un newton (masse de 1 kg possédant une accélération de 1 m.s-2) Résultat : 1 N = 1 kg.m.s-2

Et voici maintenant comment procéder pour retrouver la décomposition de chacune des autres unités de mesure :

Question : comment retrouver la décomposition d'un newton mètre ? Solution : il suffit de multiplier la décomposition du newton par 1 mètre puisque 1 N.m = 1 N x 1 m Résultat : 1 N.m = 1 kg.m2.s-2

 

Question : comment retrouver la décomposition d'un joule ? Solution : c'est la même décomposition qu'un newton mètre puisque 1 J = 1 N.m Résultat : 1 J = 1 kg.m2.s-2

 

Question : comment retrouver la décomposition d'un watt ? Solution : il suffit de diviser la décomposition du joule par 1 seconde puisque 1 W = 1 J / 1 s Résultat : 1 W = 1 kg.m2.s-3

 

Question : comment retrouver la décomposition d'un volt ? Solution : il suffit de diviser la décomposition du watt par 1 ampère puisque 1 V = 1 W / 1 A Résultat : 1 V = 1 kg.m2.A-1.s-3

 

Question : quelle est la décomposition d'un ampère ? Solution : comme l'ampère fait parti des unités de base du système international il n'a pas de décomposition Résultat : 1 ampère = 1 kg0.m0.A1.s0 = 1 A

 

Question : comment retrouver la décomposition d'un ohm ? Solution : il suffit de diviser la décomposition du volt par 1 ampère puisque 1 Ω = 1 V / 1 A Résultat : 1 Ω = 1 kg.m2.A-2.s-3

 

Question : comment retrouver la décomposition d'un siemens ? Solution : sachant que G=1/R on en déduit que le siemens est l'inverse (au sens mathématique) d'un ohm Résultat : 1 S = 1 kg-1.m-2.A2.s3

 

Question : comment retrouver la décomposition d'un farad (rappel : τ = R.C) ? Solution : il faut multiplier la décomposition du siemens par 1 seconde puisque 1 F = 1 s / 1 Ω = 1 s x 1 S Résultat : 1 F = 1 kg-1.m-2.A2.s4

 

Question : comment retrouver la décomposition d'un henry (rappel : τ = L/R) ? Solution : il faut multiplier la décomposition de l'ohm par 1 seconde puisque 1 H = 1 Ω x 1 s Résultat : 1 H = 1 kg.m2.A-2.s-2

 

Question : comment retrouver la décomposition d'un coulomb ? Solution : il suffit de multiplier 1 ampère par 1 seconde puisque 1 C = 1 A x 1 s Résultat : 1 C = 1 A.s

 

Question : comment retrouver la décomposition d'un weber ? Solution : il suffit de multiplier la décomposition du volt par 1 seconde puisque 1 Wb = 1 V x 1 s Résultat : 1 Wb = 1 kg.m2.A-1.s-2

 

Question : comment retrouver la décomposition d'un pascal ? Solution : il suffit de diviser la décomposition du newton par 1 mètre carré puisque 1 Pa = 1 N / 1 m² Résultat : 1 Pa = 1 kg.m-1.s-2

 

Question : quelle est la décomposition d'un radian par seconde ? Solution : le radian n'est pas une unité de mesure du système international (comme le tour ou la période) Résultat : 1 rad.s-1 = 1 s-1

 

Question : et pour finir quelle est la décomposition d'un hertz (rappel 1 Hz = 1 période par seconde) ? Solution : la définition du hertz nous rappelle qu'il s'agit de rien d'autre que l'inverse du temps Résultat : 1 Hz = 1 s-1

 

Récapitulatif des transformations d'une unité à l'autre

Légende : la couleur du fond indique s'il s'agit d'une unité ou d'une opération permettant de passer d'une unité à l'autre
unité	opération

A partir du newton on obtient le pascal, le newton mètre, le joule, le watt et le volt :

1 newton	→ x 1 mètre →	1 newton mètre = 1 joule	→ / 1 seconde ↓
↓/ 1 mètre carré ↓			1 watt
1 pascal			↓/ 1 ampère↓
			1 volt

A partir du volt on obtient le weber, l'ohm, le siemens, le henry et le farad :

1 volt	→ / 1 ampère →	1 ohm	→ l'inverse ↓
↓x 1 seconde ↓		↓x 1 seconde ↓	1 siemens
1 weber		1 henry	↓x 1 seconde ↓
			1 farad

Quant aux décompositions des unités suivantes elles sont immédiates :

1 ampère = 1 A

1 coulomb = 1 A.s (un coulomb est simplement un ampère seconde)

1 kilogramme = 1 kg

1 seconde = 1 s

1 mètre = 1 m

1 mètre carré = 1 m²

1 mètre par seconde = 1 m.s^-1

1 mètre par seconde carrée = 1 m.s^-2

1 radian par seconde = 1 s^-1 (le radian ne se décompose pas en unité de mesure : ce n'est pas une grandeur physique)

 

Et voilà nos 20 unités de mesure décomposées sans effort dans le système international kg m A s !

Sans oublier le hertz, qui n'est pas classé dans les 20 unités de mesure de base ci-dessus :

1 hertz = 1 s^-1

 

Mettons un peu d'ordre dans tout ça en structurant ce qu'il faut en retenir

Appelons une "unité simple" une unité qui se décompose en utilisant seulement 1 ou 2 unités de base du système international kg m A s.

Appelons une "unité composée" une unité qui se décompose en utilisant 3 ou 4 unités de base du système international kg m A s.

Sur les 20 unités de mesure des sciences de l'ingénieur étudiées ici il y a 10 unités simples et 10 unités composées.

Les 10 unités simples sont (leur définition suffit pour trouver leur décomposition) :

• le kilogramme
• le mètre
• l'ampère
• la seconde
• le mètre carré
• le mètre par seonde
• le mètre par seconde carrée
• le radian par seconde
• le hertz
• le coulomb

La seule unité composée dont la définition nous donne directement la décomposition est le Newton :

• 1 newton = 1 kilogramme possédant une accélération de 1 mètre par seconde carrée = 1 kg.m.s^-2

Les 10 unités composées suivantes se retrouvent toutes à partir de la décomposition d'un Newton :

• le pascal
• le newton mètre
• le joule
• le watt
• le volt
• l'ohm
• le siemens
• le weber
• le henry
• le farad

 

Retour au sommaire

 

Pour être capable de ressortir de tête la décomposition de chacune des 21 unités précédentes il suffit de retenir que :

1 - on part de la définition d'un newton : 1 N = 1 kg.m.s^-2

2 - le newton nous donne la décomposition des 10 unités composées comme le résume l'arbre suivant. Remarques :

• cet arbre ne contient que des unités de mesure (et non des grandeurs physiques)
• par exemple m représente un mètre (et non la masse !)
• s (en minuscule et en bleu) est une seconde et S (en majuscule et en rouge) est un Siemens
• x signifie "multiplier par" et / signifie "diviser par"

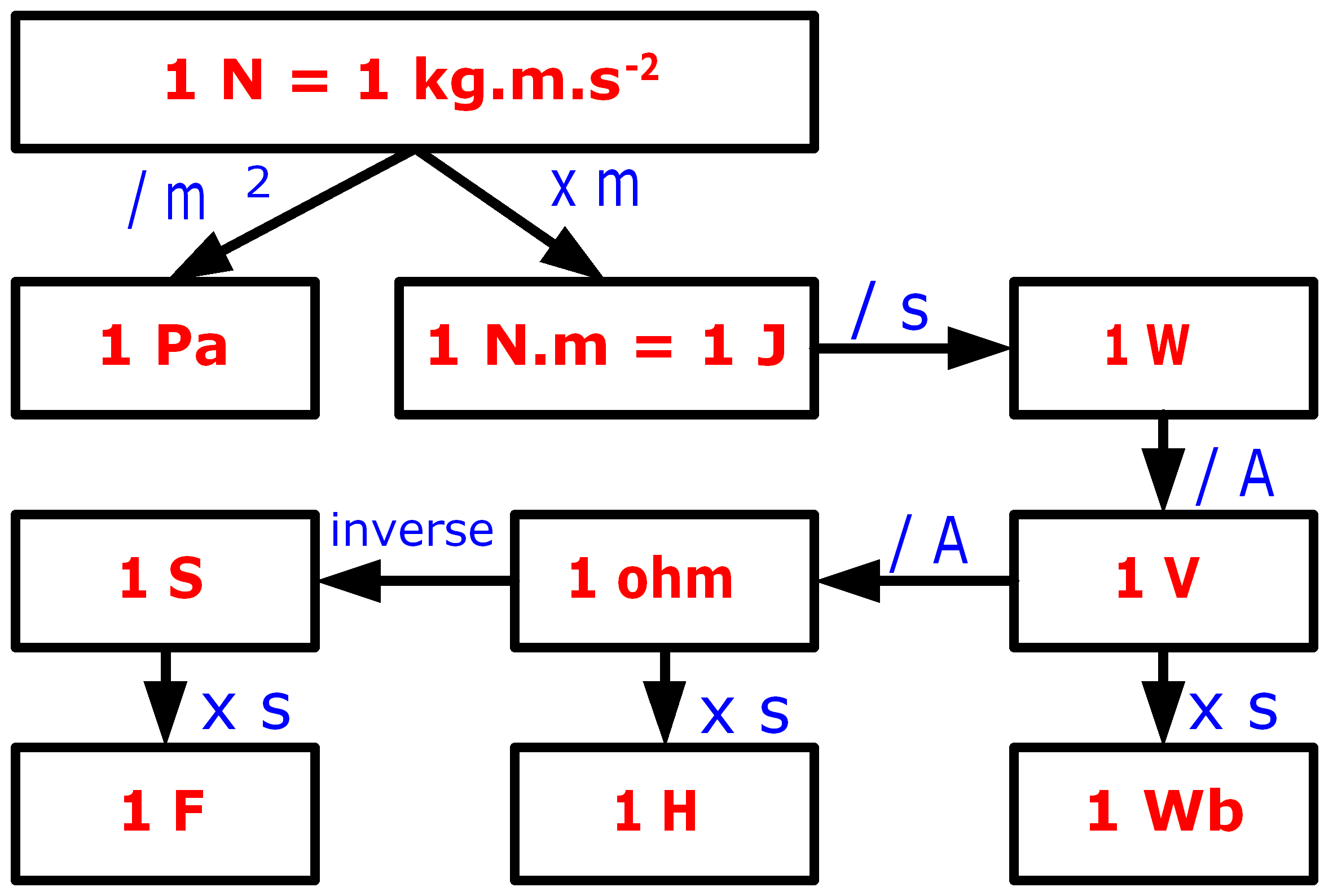
Arbre de conversion pour retrouver les 10 unités composées à partir du newton

 

3 - les 10 unités simples possèdent une décomposition immédiate (avec seulement 1 ou 2 unités de base)

Pour vous entraîner et réviser toutes ces relations dans un QCM cliquez ici (choisissez un des 2 thèmes "Les unités de mesure").

 

Retour au sommaire

 

La liste des relations vues sur cette page n'est pas exhaustive. Il existe encore beaucoup d'autres relations entre les unités ou entre les grandeurs physiques vues ici.

Par exemple en utilisant les relations données plus haut sur cette page on peut encore constater les nouvelles relations suivantes (qui ne sont pas vraiment nouvelles mais qui sont simplement la conséquence de tout ce que nous venons de remarquer) :

En remarquant que :	On peut en déduire que :	Commentaire :
1 J = 1 V.A.s et 1 A.s = 1 C	1 V = 1 J / 1 C = 1 J.C-1	des joules divisés par des coulombs donnent des volts
1 J = 1 V.A.s et 1 V.s = 1 Wb	1 A = 1 J / 1 Wb = 1 J.Wb-1	des joules divisés par des webers donnent des ampères
1 H = 1 s.Ω et 1 F = 1 s.Ω-1	1 H x 1 F = 1 s2	des henrys multipliés par des farads donnent des secondes carrées
	1 H / 1 F = 1 Ω2	des henrys divisés par des farads donnent des ohms carrés
1 h = 3600 s	1 A.h = 3600 C	un ampère heure contient 3600 coulombs
	1 V.h = 3600 Wb	un volt heure contient 3600 webers
	1 W.h = 3600 J	un watt heure contient 3600 joules
W=(C.U2)/2 et Q=C.U	W=(Q.U)/2	des coulombs multipliés par des volts donnent des joules
W=(L.I2)/2 et Φ=L.I	W=(Φ.I)/2	des webers multipliés par des ampères donnent des joules
1 Wb = 1 V.s et 1 C = 1 A.s	1 Wb.C = 1 W.s2	des webers multipliés par des coulombs donnent des watts secondes carrées

On déduit des deux premières lignes les 4 expressions suivantes correspondant toutes au joule :

1 J = 1 W.s = 1 V.A.s = 1 V.C = 1 A.Wb

Soit en clair les nouvelles relations suivantes :

1 joule = 1 volt coulomb = 1 ampère weber

Ces relations se retrouvent également dans les deux dernières lignes du tableau ci-dessus utilisant les formules de l'énergie emmagasinée dans un condensateur ou dans une bobine.

Exemples d'application :

• en divisant la réserve énergétique en joules d'une batterie par la tension en volts de cette batterie on obtient directement sa capacité en coulombs
• en multipliant la capacité en coulombs d'une batterie par la tension en volts de la batterie on obtient directement sa réserve énergétique en joules
• en multipliant par 3600 la capacité en ampères heures d'une batterie on obtient la capacité de la batterie en coulombs
• en multipliant par 3600 une énergie en watts heures on obtient cette même énergie exprimée en joules
• etc.

Et en sachant que la loi d'ohm nous dit que 1 V = 1 Ω.A (1 volt = 1 ohm ampère) soit 1 A = 1 S.V (1 ampère = 1 siemens volt) nous obtenons 4 nouvelles formes du joule en utilisant les unités seconde, volt, ampère, ohm, siemens, coulomb et weber :

1 J = 1 A².Ω.s =1 V².S.s = 1 Ω.A.C = 1 S.V.Wb

 

Or 1 Ω.s = 1 H (1 ohm seconde = 1 henry) et 1 S.s = 1 F (1 siemens seconde = 1 farad). Nous obtenons alors 2 nouvelles formes du joule utilisant cette fois le henry et le farad :

1 J = 1 A².H =1 V².F

 

Or 1 H = 1 s².F^-1 (1 henry = 1 seconde carrée par farad) et 1 F = 1 s².H^-1 (1 farad = 1 seconde carrée par henry). Nous obtenons alors 6 nouvelles formes du joule :

1 J = 1 A².s².F^-1 = 1 C².F^-1 = 1 C².H.s^-2 = 1 V².s².H^-1 = 1 Wb².H^-1 = 1 Wb².F.s^-2

 

Sachant que 1 J = 1 W.s et que 1 s = 1 C.A^-1 = 1 Wb.V^-1 = 1 F.Ω = 1 H.Ω^-1 = 1 H.S que il vient alors 5 formes du joule en fonction du watt :

1 J = 1 W.C.A^-1 = 1 W.Wb.V^-1 = 1 W.F.Ω = 1 W.H.Ω^-1 = 1 W.H.S

 

En remarquant que 1 Wb.C = 1 V.s.A.s = 1 W.s² (1 weber coulomb = 1 watt seconde carrée) on peut également écrire que :

1 J = 1 Wb.C.s^-1

 

Et comme en mécanique on a aussi 1 J = 1 N.m soit 1 J = 1 kg.m².s^-2 nous pouvons donner pas moins de 24 unités composées toutes équivalentes au joule utilisant chacune moins de 4 unités dérivées du système international. Les voici :

Les 24 unités de mesure équivalentes au joule
Nom de l'unité de mesure	Symbole de l'unité de mesure
watt seconde	W.s
volt ampère seconde	V.A.s
volt coulomb	V.C
ampère weber	A.Wb
ohm ampère coulomb	Ω.A.C
siemens volt weber	S.V.Wb
ampère carré ohm seconde	A2.Ω.s
volt carré siemens seconde	V2.S.s
ampère carré henry	A2.H
volt carré farad	V2.F
ampère carré seconde carrée par farad	A2.s2.F-1
coulomb carré par farad	C2.F-1
volt carré seconde carrée par henry	V2.s2.H-1
weber carré par henry	Wb2.H-1
henry coulomb carré par seconde carrée	H.C2.s-2
farad weber carré par seconde carrée	F.Wb2.s-2
watt coulomb par ampère	W.C.A-1
watt weber par volt	W.Wb.V-1
watt farad ohm	W.F.Ω
watt henry par ohm	W.H.Ω-1
watt henry siemens	W.H.S
weber coulomb par seconde	Wb.C.s-1
newton mètre	N.m
kilogramme mètre carré par seconde carrée	kg.m2.s-2

Enfin, comme nous l'a montré l'arbre de conversion plus haut, on peut également remarquer que la plupart des grandeurs électriques peuvent s'exprimer en fonction du temps et d'une autre unité :

Unité :	Unité équivalente :	Expression correspondante :
le joule	le watt seconde	1 J = 1 W.s
le coulomb	l'ampère seconde	1 C = 1 A.s
le weber	le volt seconde	1 Wb = 1 V.s
le henry	l'ohm seconde	1 H = 1 Ω.s
le farad	le siemens seconde	1 F = 1 S.s

 

Pour vous entraîner et réviser toutes ces relations dans un QCM cliquez ici (choisissez un des 2 thèmes "Les unités de mesure").

 

Retour au sommaire

 

La puissance (en Watt) est toujours égale au produit d'une grandeur d'effort (force, couple, pression, tension, etc.) par une grandeur de flux (vitesse linéaire, vitesse angulaire, débit, intensité du courant, etc.).

Grandeur d'effort

Une grandeur d'effort est, dans le domaine physique, une grandeur qui "tend" à déplacer de la matière ou quelque chose qui en tient lieu. Au premier degré, la tension électrique, la force mécanique, le couple, la température, la pression acoustique, la pression hydraulique, le potentiel magnétique sont des grandeurs d'effort.

Grandeur de flux

Une grandeur de flux est, dans le domaine physique, une grandeur qui traduit un déplacement de matière ou de quelque chose qui en tient lien avec un certain "débit". Au premier degré, le courant électrique, la vitesse de translation, la vitesse de rotation, le flux de chaleur, la vitesse acoustique, le débit hydraulique, le flux magnétique sont des grandeurs de flux.

Voici les grandeurs d'effort et de flux dont le produit donne différents types de puissance :

Puissance	Grandeur d'effort	Grandeur de flux
Puissance électrique (W)	tension (V)	courant (A)
Puissance mécanique en translation (W)	force (N)	vitesse linéaire (m.s-1)
Puissance mécanique en rotation (W)	couple (N.m)	vitesse angulaire (rd.s-1)
Puissance pneumatique (W)	pression (Pa)	débit (m3.s-1)
Puisance hydraulique (W)	pression (Pa)	débit (m3.s-1)

Les constituants de la chaîne d'énergie sont reliés entre eux par un lien de puissance (demi-flèche) transportant les deux grandeurs, effort e et flux f, dont le produit caractérise le transfert de puissance entre ces constituants. Quand on souhaite préciser les deux grandeurs précédentes sur un lien de puissance, la notation est la suivante :

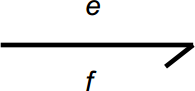
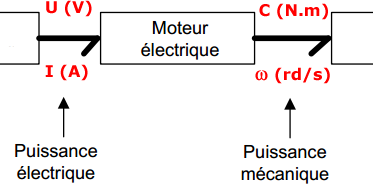
Exemple de représentation de la chaîne d'énergie à l'entrée et en sortie d'un moteur électrique : on y distingue les deux grandeurs physiques (grandeur d'effort au dessus et grandeur de flux en dessous de la demi-flèche) dont le produit est égal à la puissance transmise :

 

 

Retour au sommaire

 

Certaines unités de mesure du système international ne correspondent pas à l'échelle de leur utilisation, et paraissent soit beaucoup trop grandes (ex : le mètre carré pour mesurer la surface de la tige d'un vérin) soit beaucoup trop petite (ex : le pascal pour mesurer la pression dans un système pneumatique de puissance).

Pour cette raison de nouvelles unités, multiples ou sous-multiples directs des unités de base, sont souvent utilisées dans des domaines bien précis.

Si cette unité de base est trop petite	on les regroupe par paquet de	et on appelle l'ensemble	Relation à connaître
le kilogramme (masse)	1 000 kg	1 tonne	1 000 kg = 1 t
la seconde (temps)	60 s	1 minute	60 s = 1 min
la seconde (temps)	3 600 s	1 heure	3 600 s = 1 h
le mètre carré (surface)	100 m²	1 are	100 m² = 1 are
le mètre carré (surface)	10 000 m²	1 hectare	10 000 m² = 1 ha
le Pascal (pression)	100 000 Pa	1 bar	100 000 Pa = 1 bar
le newton (force)	10 N	1 décanewton	10 N = 1 daN
le joule (énergie)	3 600 J	1 wattheure	3 600 j = 1 W.h
le radian (angle)	2.π radians	1 tour	2.π rad = 1 tr

 

Si cette unité de base est trop grande	on la divise en	et on appelle chaque portion	Relation à connaître
le mètre (longueur)	1 000	1 millimètre	1 m = 1 000 mm
le mètre carré (surface)	10 000	1 centimètre carré	1 m² = 10 000 cm²
le mètre carré (surface)	1 000 000	1 millimètre carré	1 m² = 1 000 000 mm²
le mètre cube (volume)	1 000	1 litre	1 m3 = 1 000 l

Exemple d'application :

Quelle est la force fournie par un vérin recevant une pression de 6 Pascal sur une surface active de 3 m² ?

Réponse instantanée : F = p.S donc F = 6x3 = 18 Newton, mais ces valeurs ne sont pas très réalistes.

Autre exemple plus réaliste :

Quelle est la force fournie par un vérin recevant une pression p de 7 Bar sur une surface active S de 4 cm² ?

Convertissons la pression en Pascal :

p = 7 bar = 7.10⁵ Pa

Convertissons la surface en mètre carré :

S = 4 cm² = 4.10^-4 m²

F = p.S donc F = 7.10⁵ x 4.10^-4 = 7x4x10 = 280 N = 28 daN

A retenir :

Comme 1 bar = 10⁵ Pa et 1 cm² = 10^-4 m² on remarque qu'en multipliant des Bar par des cm² on n'obtient pas directement des Newton mais des dizaines de Newton.

Comme 10 N = 1 daN, pour éviter les calculs avec les puissances de 10 on retiendra que des bar multipliés par des cm² donnent directement des décaNewton.

Exemple :

Quelle est la force fournie par un vérin recevant une pression de 3 Bar sur une surface active de 2 cm² ?

Réponse instantanée : 6 daN car F = p.S avec F en daN, p en bar et S en cm².

 

Conversion des unités de mesure de la vitesse angulaire

L'unité de mesure de base de la vitesse angulaire dans le système international est le radian par seconde. Mais sachant qu'il y a 60 secondes dans une minute et 2.π radians dans un tour, il en résulte 4 unités de mesure dont la conversion est résumée dans les deux graphes suivants :

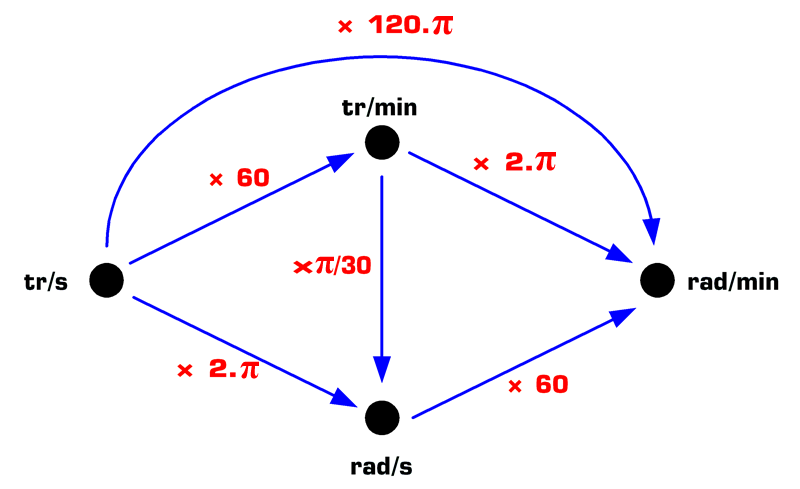
Les conversions inverses se font naturellement en effectuant une division à la place des multiplications :

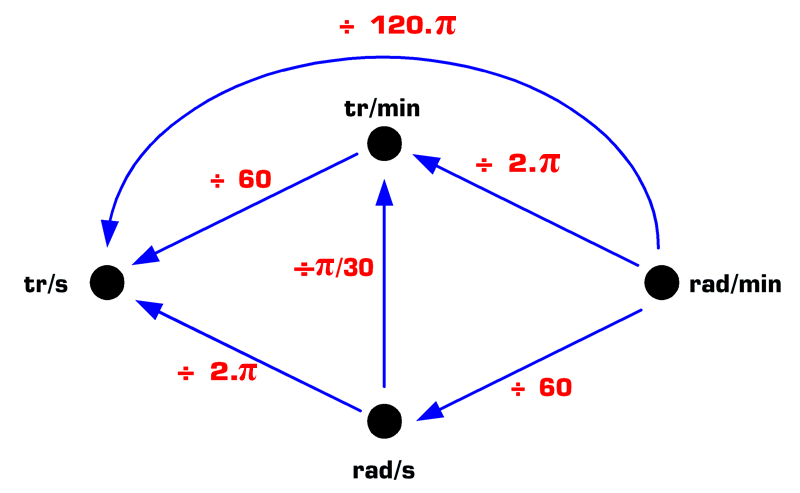
Ces graphes de conversions permettent d'effectuer de tête et instantanément une estimation de la vitesse angulaire en prenant comme valeur arrondie 3 pour π :

Valeur exacte	Valeur approximative pour les calculs de tête
π	3
2.π	6
120.π	360
π/30	1/10

Voici les 8 opérations en nombres entiers pour estimer rapidement une valeur :

Opération exacte	Opération simplifiée pour estimation
multiplier par π	× 3
multiplier par 2.π	× 6
multiplier par 120.π	× 360
multiplier par π/30	÷ 10
diviser par π	÷ 3
diviser par 2.π	÷ 6
diviser par 120.π	÷ 360
diviser par π/30	× 10

Et voici les 8 opérations possibles, en nombres entiers, à effectuer pour estimer de tête la valeur d'une vitesse angulaire en changeant d'unité de mesure et en utilisant les 12 conversions données dans les deux graphes ci-dessus :

Pour convertir des	en	il faut	Opération simplifiée :
tour par seconde	tour par minute	multiplier par 60	× 60
radian par seconde	radian par minute
tour par seconde	radian par seconde	multiplier par 2.π	× 6
tour par minute	radian par minute
tour par seconde	radian par minute	multiplier par 120.π	× 360
tour par minute	radian par seconde	multiplier par π/30	÷ 10
tour par minute	tour par seconde	diviser par 60	÷ 60
radian par minute	radian par seconde
radian par seconde	tour par seconde	diviser par 2.π	÷ 6
radian par minute	tour par minute
radian par minute	tour par seconde	diviser par 120.π	÷ 360
radian par seconde	tour par minute	diviser par π/30	× 10

Comment retenir tout ça ? Tout simplement en se représentant le graphe de conversion ci-dessous rappelant seulement les conversions multiplicatives avec les valeurs arrondies (pour faire une conversion dans le sens inverse d'une flèche il suffit d'effectuer une division à la place d'une multiplication) :

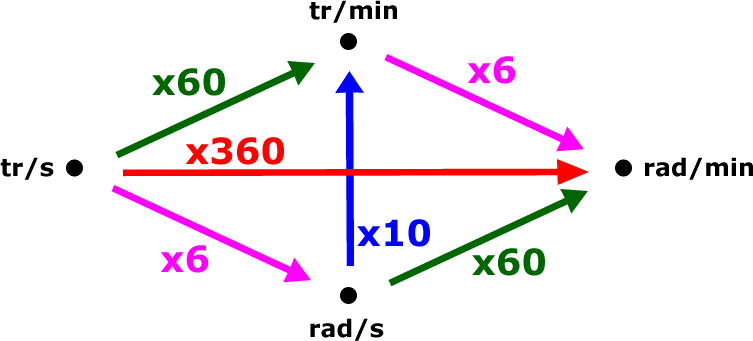
Graphe de conversion simplifié

1^er exemple d'application :

Question : quelle est la valeur approchée en tr/min d'une vitesse angulaire de 43 rad/s ?

Réponse instantanée : environ 430 tr/min car pour passer des radians par seconde aux tours par minute il faut simplement multiplier par 10 environ.

 

2^ème exemple d'application :

Question : quelle est la valeur approchée en tr/min d'une vitesse angulaire de 240 rad/min ?

Réponse instantanée : environ 40 tr/min car pour passer des radians par minute aux tours par minute il faut diviser par 6 environ.

 

3^ème exemple d'application :

Problème : classer ces 4 vitesses de rotation dans l'ordre croissant :

• v1 = 10 tr/s
• v2 = 10 tr/min
• v3 = 10 rad/s
• v4 = 10 rad/min

Solution : pour comparer des vitesses de rotation il faut toutes les convertir dans la même unité en utilisant le graphe de conversion simplifié. Si on veut effectuer seulement des multiplications, le graphe de conversion simplifié nous indique de tout convertir en radian par minute :

• v1 = 10 tr/s = 10x360 rad/min = 3600 rad/min
• v2 = 10 tr/min = 10x6 rad/min = 60 rad/min
• v3 = 10 rad/s = 10x60 rad/min = 600 rad/min
• v4 = 10 rad/min

Les 4 vitesses étant toutes exprimées en radians par minute on peut maintenant les comparer et les classer dans l'ordre croissant (de la plus petite à la plus grande) :

v4 < v2 < v3 < v1

A retenir :

1 rad/min < 1 tr/min < 1 rad/s < 1tr/s

 

4^ème exemple d'application :

Problème : classer ces 4 vitesses de rotation dans l'ordre décroissant :

• v1 = 16.9 rad/s
• v2 = 297.1 tr/min
• v3 = 2.3 tr/s
• v4 = 324 rad/min

Solution : pour comparer ces vitesses de rotation il faut avant tout les convertir dans une seule unité de mesure (par exemple le radian par minute si on veut effectuer seulement des multiplications dont l'estimation du résultat peut se faire de tête) :

• v1 = 16.9 rad/s = 16.9x60 rad/min = 1014 rad/min
• v2 = 297.1 tr/min = 297.1x6 rad/min = 1782.6 rad/min
• v3 = 2.3 tr/s = 2.3x360 rad/min = 828 rad/min
• v4 = 324 rad/min

Les 4 vitesses étant toutes exprimées en radians par minute on peut maintenant les comparer et les classer dans l'ordre décroissant (de la plus grande à la plus petite) :

v2 > v1 > v3 > v4

Soit avec les valeurs de l'énoncé :

297.1 tr/min > 16.9 rad/s > 2.3 tr/s > 324 rad/min

 

Remarque concernant les valeurs approchées données par le graphe de conversion simplifié :

Lorsqu'on utilise le graphe de conversion simplifié afin d'avoir juste un ordre d'idée du résultat (et non une valeur exacte) il ne faut pas oublier concernant les coefficients multiplicatifs que :

• 6 est une valeur approchée de 2.π et que 6 < 2.π
• 360 est une valeur approchée de 120.π et que 360 < 120.π
• 10 est une valeur approchée de 30/π et que 10 > 30/π
• 60 est une valeur exacte

Chacun en déduira si les résultats donnés par le graphe de conversion simplifié sont des valeurs par défaut, par excès ou exactes.

 

Retour au sommaire

 

Les tableaux suivants donnent la décomposition des unités de mesure de 36 grandeurs physiques dans le système international (kg m A s).

 

Les 19 grandeurs électriques : elles contiennent de l'ampère dans leur décomposition

Symbole de la grandeur	Nom de la grandeur	Nom de l'unité de mesure	Symbole de l'unité de mesure	Décomposition de l'unité de mesure dans le système international
U	tension	volt	V	kg.m2.A-1.s-3
I	courant	ampère	A	A
R	résistance	ohm	Ω	kg.m2.A-2.s-3
G	conductance	siemens	S	kg-1.m-2.A2.s3
X	réactance	ohm	Ω	kg.m2.A-2.s-3
B	susceptance	siemens	S	kg-1.m-2.A2.s3
Z	impédance	ohm	Ω	kg.m2.A-2.s-3
Y	admittance	siemens	S	kg-1.m-2.A2.s3
ρ	résistivité	ohm mètre	Ω.m	kg.m3.A-2.s-3
γ	conductivité	siemens par mètre	S.m-1	kg-1.m-3.A2.s3
C	capacité	farad	F	kg-1.m-2.A2.s4
L	inductance	henry	H	kg.m2.A-2.s-2
Q	quantité d’électricité	coulomb	C	A.s
Φ	flux magnétique	weber	Wb	kg.m2.A-1.s-2
T	période	seconde	s	s
f	fréquence	hertz	Hz	s-1
ω	pulsation	radian par seconde	rad.s-1	s-1
φ	phase à l’origine	radian	rad	sans unité
φ u/i	déphasage	radian	rad	sans unité

 

Les 17 grandeurs mécaniques : elles ne contiennent pas d'ampère dans leur décomposition

Symbole de la grandeur	Nom de la grandeur	Nom de l'unité de mesure	Symbole de l'unité de mesure	Décomposition de l'unité de mesure dans le système international
t	temps	seconde	s	s
l	longueur	mètre	m	m
S	surface	mètre carré	m2	m2
V	volume	mètre cube	m3	m3
P	puissance	watt	W	kg.m2.s-3
W	énergie	joule	J	kg.m2.s-2
F	force	newton	N	kg.m.s-2
p	pression	pascal	Pa	kg.m-1.s-2
c	couple	newton mètre	N.m	kg.m2.s-2
M	moment	newton mètre	N.m	kg.m2.s-2
v	vitesse linéaire	mètre par seconde	m.s-1	m.s-1
a	accélération linéaire	mètre par seconde carrée	m.s-2	m.s-2
Ω	vitesse angulaire	radian par seconde	rad.s-1	s-1
γ	accélération angulaire	radian par seconde carrée	rad.s-2	s-2
k	raideur d'un ressort	newton par mètre	N.m-1	kg.s-2
q	quantité de mouvement	newton seconde	N.s	kg.m.s-1
J	moment d'inertie	kilogramme mètre carré	kg.m2	kg.m2

Enfin, en comparant la décomposition des grandeurs électriques et mécaniques on peut retrouver des liens entre deux grandeurs physiques de nature différente et qui ont seulement l'ampère comme écart dans leur décomposition :

1 henry = 1 joule par ampère carré

1 weber = 1 joule par ampère

1 volt = 1 watt par ampère

 

⇒ Télécharger la fiche pratique en PDF récapitulant la décomposition de 30 unités de mesure

⇒ Télécharger la fiche pratique en PDF "Les 24 grandeurs physiques utilisées en électronique" avec un formulaire complet

 

Retour au sommaire

 

Voici quelques compléments concernant les unités de mesure utilisés en physique-chimie et non en sciences de l'ingénieur. Ces unités peuvent concerner des domaines comme la température, la lumière, la quantité de matière, l'électromagnétisme ou la radioactivité par exemple (et non seulement l'électricité et la mécanique qui sont les deux seuls domaines développés ci-dessus dans le cadre des sciences de l'ingénieur).

Le lux est une unité de mesure de l'éclairement lumineux. (symbole : lx) Il caractérise le flux lumineux reçu par unité de surface. Un lux est l'éclairement d'une surface qui reçoit, d'une manière uniformément répartie, un flux lumineux par mètre carré.

Le calcul est le suivant: 1lx = 1 lm/m² = 1 cd.sr/m² car 1 lm = 1 cd.sr

Avec: lm: lumen (unité de mesure de flux lumineux) ; sr: stéradian (unité de mesure d'angle solide) ; cd: candela (unité de mesure d'intensité lumineuse) ; m (mètre).

Quelques définitions autour des unités relatives à la lumière :

⇒ flux lumineux : les lumens indiquent la quantité totale de lumière émise par une source lumineuse, dans toutes les directions à la fois;

⇒ intensité lumineuse : les candelas désignent la quantité de lumière émise dans une direction donnée;

⇒ luminance : les candelas/m² permettent de rendre compte de la luminosité de la surface (par exemple, le filament d’une lampe à incandescence est très brillant, tandis que si l’ampoule est dépolie, on sera moins ébloui);

⇒ éclairement : les lux représentent la quantité de lumière reçue sur une surface, sans aucune indication de la source lumière elle-même (qui peut être aussi bien faiblarde mais proche que très puissante mais lointaine).

En réalité le système internationnal d'unités de mesure ne contient pas seulement les 4 unités de base vues en sciences de l'ingénieur (kilogramme ampère seconde et mètre) mais contient 7 unités de base : il faut y ajouter le kelvin, la mole et la candela.

Voici la définition de ces 3 nouvelles unités de mesure de base :

⇒ Le kelvin (K), unité de température thermodynamique, est la fraction 1/273,16 de la température thermodynamique du point triple de l'eau.

⇒ La mole (mol) est la quantité de matière d'un système contenant autant d'entités élémentaires qu'il y a d'atomes dans 0,012 kilogramme de carbone 12.

⇒ La candela (cd) est l'intensité lumineuse, dans une direction donnée, d'une source qui émet un rayonnement monochromatique de fréquence 540×1012 s-1 (hertz) et dont l'intensité énergétique dans cette direction est de 1/683 watt par stéradian.

Comme vu pour les unités utilisés en sciences de l'ingénieur ces 3 nouvelles unités de base donnent naissances à plusieurs dizaines d'unités dérivées, possédant de multiples liens entre elles. Voici quelques exemples de grandeurs physiques et d'unités de mesure complémentaires à celles vues dans le cadre des sciences de l'ingénieur :

Nom de la grandeur physique	Nom de l'unité de mesure	Symbole de l'unité de mesure	Unité de mesure équivalente	Décomposition de l'unité de mesure dans le système international
température	kelvin	K	°C+273.15	K
masse volumique	kilogramme par mètre cube	kg.m-3		kg.m-3
énergie massique	joule par kilogramme	J.kg-1		m2.s-2
capacité thermique massique (ou chaleur massique ou chaleur spécifique)	joule par (kilogramme-kelvin)	J.kg-1.K-1		m2.s-2.K-1
induction magnétique	tesla	T	Wb.m-2	kg.A-1.s-2
angle solide	stéradian	sr		sans unité
flux lumineux	lumen	lm	cd.sr	cd
éclairement lumineux	lux	lx	lm.m-2	m-2.cd
luminance	candela par mètre carré	cd.m-2	lx.sr-1	m-2.cd
irradiance	watt par mètre carré	W.m-2		kg.s-3
quantité de matière	mole	mol		mol
masse molaire	kilogramme par mole	kg.mol-1		kg.mol-1
conductivité thermique	watt par (mètre-kelvin)	W.m-1.K-1		kg.m.s-3.K-1
conductance thermique	watt par kelvin	W.K-1		kg.m2.s-3.K-1
résistance thermique surfacique	mètre carré-kelvin par watt	m2.K.W-1		kg-1.s3.K
activité radioactive	becquerel	Bq	s-1	s-1
débit de dose radioactive	sievert	Sv	J.kg-1	m2.s-2

Les unités dérivées cohérentes sont définies de manière unique et seulement en fonction des unités de base du système international. Par exemple, l’unité cohérente dérivée de résistance, l’ohm, symbole Ω, est définie de manière unique par la relation Ω = m² kg s^–3 A^–2, qui résulte de la définition de la grandeur résistance. Cependant, il est possible d’utiliser n’importe quelle méthode en accord avec les lois de la physique pour réaliser n’importe laquelle des unités de mesure. En pratique, l’unité ohm peut être réalisée avec une exactitude élevée au moyen de l’effet Hall quantique et de la valeur de la constante de von Klitzing recommandée par le Comité international.

Enfin, il faut reconnaître que même si les sept grandeurs de base – longueur, masse, temps, courant électrique, température thermodynamique, quantité de matière et intensité lumineuse – sont considérées comme indépendantes par convention, les unités de base – le mètre, le kilogramme, la seconde, l’ampère, le kelvin, la mole et la candela – ne le sont pas. Ainsi la définition du mètre fait appel à la seconde ; la définition de l’ampère fait appel au mètre, au kilogramme et à la seconde ; la définition de la mole fait appel au kilogramme ; et la définition de la candela fait appel au mètre, au kilogramme et à la seconde.

⇒ Pour aller plus loin consultez ce document PDF de 186 pages établi par le Bureau International des Poids et Mesures

 

Retour au sommaire

 

Voici la liste des 16 physiciens qui ont laissé leur nom dans l'histoire en le donnant, suite aux travaux qu'ils ont effectués, aux unités de mesure que nous utilisons aujourd'hui. Ce tableau est trié dans l'ordre chronologique des années de naissance et un lien est disponible en cliquant sur le nom des physiciens :

Nom de l'unité de mesure	Nom du physicien	Nationalité	Période
pascal	Blaise Pascal	français	1623 - 1662
newton	Isaac Newton	britannique	1643 - 1727
degré celsius	Anders Celsius	suédois	1701 - 1744
coulomb	Charles-Augustin Coulomb	français	1736 - 1806
watt	James Watt	écossais	1736 - 1819
volt	Alessandro Volta	italien	1745 - 1827
ampère	André-Marie Ampère	français	1775 - 1836
ohm	Georg Ohm	allemand	1789 - 1854
farad	Michael Faraday	britannique	1791 - 1867
henry	Joseph Henry	américain	1797 - 1878
weber	Wilhelm Eduard Weber	allemand	1804 - 1891
siemens	Werner von Siemens	allemand	1816 - 1892
joule	James Prescott Joule	britannique	1818 - 1889
kelvin	Lord Kelvin	britannique	1824 - 1907
tesla	Nikola Tesla	serbe	1856 - 1943
hertz	Heinrich Rudolf Hertz	allemand	1857 - 1894

Remarque : le nom des unités de mesure de base (mètre, seconde, gramme, candela, etc.) sont en général dérivés de la traduction d'anciennes locutions grecques ou latines, et non du nom d'un physicien comme le sont les unités de mesure plus modernes. Exemple : la candela vient de la traduction du mot "chandelle" (d'où un nom d'unité féminin).